Hamming Codes: What Multiple Parity Bits Can Do

     Hamming Codes are built upon the idea of using Parity Bits to detect errors. If we instead included two parity bits, one for the first half of the data string and the other for the second half, then we would be able to not only detect whether an error has occurred, but also in which half of the data the error occurred. In this way, a second parity bit could help us get closer to locating the error. In fact, for our time of day codes (that have eleven message bits), we only need a total of five parity bits to be able to pinpoint the exact bit where an error occurred! (These five parity bits include the reddish-pink overall parity bit that you are used to by now. We will have to update that parity bit after attaching the other four, just to make sure the overall parity is still even.)

     In general, only n+1 parity bits are needed to fully protect a code with (2^n) - (n+1) data digits. In total, the protected data string will be 2^n bits long. In our practice time of day codes, we will need five parity bits. In total, our protected practice codes will be sixteen digits long. We will have to follow very carefully the following rules to create our protected code:

     Let the 11 bits of message data be denoted as D0 to D10, with D0 being the rightmost message bit and D10 being the leftmost message bit.. Let the addended bits be denoted as P0 to P4, from left to right the sequence being P4, P3, P2, P1, P0. For clarity, message bits will be black, the overall parity bit that we have already worked with will be reddish-pink and will be P4, and the new parity bits will be blue and will be P3, P2, P1, and P0. See the sample string below:

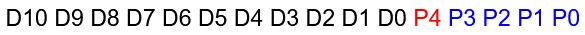
Each of the addended bits will be a parity bit, but most will only be a parity bit on a specific subset of the block:

• P0 will be a parity bit that ensures parity in only a certain half of the data, specifically the half that consists of P0, D0, D1, D3, D4, D6, D8, and D10.
• P1 will be a parity bit that ensures parity in only a certain half of the data, specifically the half that consists of P1, D0, D2, D3, D5, D6, D9, and D10.
• P2 will be a parity bit that ensures parity in only a certain half of the data, specifically the half that consists of P2, D1, D2, D3, D7, D8, D9, and D10.
• P3 will be a parity bit that ensures parity in only a certain half of the data, specifically the half that consists of P3, D4, D5, D6, D7, D8, D9, and D10.
• P4 will be an overall parity bit to quickly check for any errors, and will be updated very last.

To make clear why these specific halves were selected to correspond to each parity bit, let's arrange the 11 message bits and the 5 parity bits into a grid:

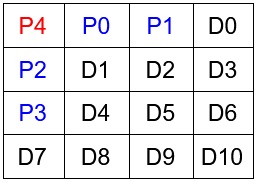
• The bit P0 corresponds to checking parity for the second and fourth columns.
• The bit P1 corresponds to checking parity in the third and fourth columns.
• The bit P2 corresponds to checking parity for the second and fourth rows.
• The bit P3 corresponds to checking parity for the third and fourth rows.

Say for example there was an error in D5. (The overall parity would then be odd). To detect and locate and correct the error:

1. The reciever first counts the number of ones to check the parity and finds an odd number of ones. The receiver now knows that an error has occurred.
2. Looking for the error, the receiver starts performing parity checks on the individual halves as determined above, starting with the two parity checks for the columns (with P0 and P1). . The error in D5 would appear in column 2. So the parity check for P0 would fail, but the parity check for P1 would succeed. Combining the two parity checks, the receiver can know that the error is not in columns 3 or 4, but only in column 2.
3. The receiver then performs the parity checks for the rows (with P2 and P3). The parity check for P2 would succeed, but the parity check for P3 would fail, meaning that the error must be found not in rows 2 or 4, but only in row 3.
4. The receiver now knows exactly which column and exactly which row the error occurred, and is free to flip the offending bit back to its intended state, thereby correcting the erroneous message.

Try generating your five parity bits all on your own. Be sure to do P4 very last, as this parity bit established even parity over the entire message (after the other parity bits are determined). Then, compare your result with the automatically generated hamming code using the applet below. Be sure to read the instructions on the applet.

For a more detailed worksheet going through Hamming Code generation on paper, you can download this tasksheetthis tasksheet.

Historical Conclusion

The Extended Hamming Code (which was presented above) was Richard Hamming's (and the world's) first Error Correcting Code.

     Richard Hamming won the 1969 Turing Award for his development of the Hamming Code. With decades of further development of computer science and code theory, a convention called "perfect codes" has been made, which describes a set of codes that are able to error protect any string without fail. Perfect codes are extremely rare, but the Hamming Code was not only the first error protecting code to be developed, but also the first perfect code to be developed.



     The Hamming Code is remarkably efficient for its protection capabilities. Although more modern and slightly more efficient codes have been developed, Hamming codes are still very applicable in many computer engineering and pedagogical circumstances. The makers of the first versions of the internet protected their data packets with hamming codes. Covert communication through steganography in images (where messages are embedded into slight changes in pixel color that are generally unnoticeable) requires extensive use of Hamming Codes (Wang) (Lee). In a similar way images can be authenticated (i.e. checked for photoshopping) by using hamming codes (Chan), and 3D models can be invisibly watermarked with the author's signature (Jen-Tse). To ensure accuracy and reliability of measurements, Hamming codes are implemented into digital calipers and digital angle calipers (Ojiganov). ISBN numbers and everyday barcodes use a Base-10 version of the parity bit, such that their left-most digit is the sum of the other digits mod 10. Hamming codes prevent errors in communication and storage on soon-to-be prevalent micro-satellites (Hillier). For more sensitive data sets, the blocks themselves can be protected in a manner similar to Hamming Codes that can identify when an egregious burst error of hundreds of bits has occurred, but the code cannot fix such an error (Das).

     But what are the downsides of the Hamming Code? Well, since the 1950s, slightly more efficient Error Correcting Codes have been developed, so those are most often used in internet communication today. In Hamming's defense, though, the newer codes are indeed more efficient, but only barely so. Additionally, these newer codes are rather esoteric, even to college-educated computer scientists. Hamming codes are generally the best introduction to ECC for college and high-school students.

     Hamming codes also have the major weakness of multiple-error failures. Hamming codes are perfect at correcting single bit errors, and will always detect (but not fix) double bit errors. But for a three-fold or more-fold bit error, Hamming codes will actually corrupt the message even more (Stakhov). For many applications, multiple-bit errors are very uncommon, but obviously "very uncommon" doesn't mean "impossible". Therefore, Hamming codes are generally inadequate for critical mission systems, in which communications failure can lead to catastrophic outcomes (i.e. in file databases, in powerplant computer systems, etc.) (Stakhov). For the same reason, Hamming codes are inadequate when communication occurs over noise-heavy lines. In these two examples, less efficient but more powerful data protection and error correction schemes must be implemented to essentially ensure preservation of communications.

     In any case, the legacy of Richard Hamming and his Hamming Codes cannot be understated. The development of Hamming Codes was perhaps the most glorious entry into a new realm of science that the human race has ever seen. Data protection and error correction will never be the same, and modern communication accuracy owes itself to Hamming Codes.




References:

Budd, C. (2018, April 17). Error Correcting Codes. Retrieved from https://plus.maths.org/content/error-correcting-codes

Chan, C.-S. (2011). An image authentication method by applying Hamming code on rearranged bits. Pattern Recognition Letters, 32(14), 1679-1690. https://doi-org.dist.lib.usu.edu/10.1016/j.patrec.2011.07.023

Das, P. K. (2018). Error Locating Codes and Extended Hamming Code. Matematicki Vesnik, 70(1), 89-94.

Gedda, Rodney. "CIO Blast from the Past: 60 Years of Hamming Codes." Computerworld, CIO, 26 Nov. 2010, www.computerworld.com/article/2514335/cio-blast-from-the-past--60-years-of-hamming-codes.html.

Hillier, C., & Balyan, V. (2019). Error Detection and Correction On-Board Nanosatellites Using Hamming Codes. Journal of Electrical & Computer Engineering, 1-15. https://doi-org.dist.lib.usu.edu/10.1155/2019/3905094

Jen-Tse Wang, Yi-Ching Chang, Chun-Yuan Yu, & Shyr-Shen Yu. (2014). Hamming Code Based Watermarking Scheme for 3D Model Verification. Mathematical Problems in Engineering, 1-7. https://doi-org.dist.lib.usu.edu/10.1155/2014/241093

Lee, C.-F., Chang, C.-C., Xie, X., Mao, K., & Shi, R.-H. (2018). An adaptive high-fidelity steganographic scheme using edge detection and hybrid hamming codes. Displays, 53, 30-39. https://doi-org.dist.lib.usu.edu/10.1016/j.displa.2018.06.001

Normand, Eugene. Single Event Upset at Ground Level. Boeing Defense and Space Group, Seattle, WA 98124-2499, https://web.archive.org/web/20131021190327/http://pdf.yuri.se/files/art/2.pdf

Ojiganov, A. (2015). The Use of Hamming Codes in Digital Angle Converters Based on Pseudo-Random Code Scales. Measurement Techniques, 58(5), 512-519. https://doi-org.dist.lib.usu.edu/10.1007/s11018-015-0746-7

Stakhov, A. (2018). Mission-Critical Systems, Paradox of Hamming Code, Row Hammer Effect, "Trojan Horse" of the Binary System and Numeral Systems with Irrational Bases. Computer Journal, 61(7), 1038-1063. https://doi-org.dist.lib.usu.edu/10.1093/comjnl/bxx083

Wang, Y., Tang, M., & Wang, Z. (2020). High-capacity adaptive steganography based on LSB and Hamming code. Optik - International Journal for Light & Electron Optics, 213, N.PAG. https://doi-org.dist.lib.usu.edu/10.1016/j.ijleo.2020.164685