Binary Review and Parity Bits

To help you better understand parity bits, we will guide you through protecting your own code with a parity bit. To do this, we need you to fully understand how to interconvert between base 10 and Binary (Base 2). Try practicing on the base 10 numbers given in the figure on the right. If you need a refresher on converting between Base 10 and Binary, the internet is at your disposal.
Now, you'll need some message to practice on. We'll use a time of day as a short message. This time of day will have a number of the hour (1-12), a number for the minute (0-59) and a AM/PM indicator. Choose a time of day for yourself, and write it down. You will convert you chosen time of day into a binary code, with the following key:
- Your binary code will contain 11 data digits.
- The left-most digit of the code will indicate the AM/PM state. Let "0" indicate AM, and let "1" indicate PM.
- The next four digits will be the hour you chose, but in Binary (Base 2). You'll have to convert the hour into Binary yourself.
- The remaining six digits will be the minute you chose, but in Binary. You'll have to convert the minute into Binary yourself.
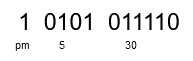
As an example, I have chosen the time of day of 5:30pm. The left-most digit will be a "1", indicating PM. The next four digits are "0101", which is the hour 5 in Binary. The remaining six digits are "011110", which is the minute 30 in Binary.
You should by now have an 11-digit binary code that represents the time of day that you chose. If you were to send this code electronically to a friend, he or she will most likely receive it with no errors in transmission. But there is a slight chance that one of the digits gets corrupted. When a binary digit is corrupted, it is called "flipping the bit", because the 1 flips to a 0 (if the bit was supposed to be a 1), or the 0 flips to a 1 (if the bit was supposed to be a 0).
If an error does occur in transmission and one of the bits in the message gets flipped, your friend will decode the Binary and read off the incorrect time of day (for example, my friend might read 8:30pm instead of my intended 5:30pm). This is obviously undesirable, and in communication, downright unacceptable.
There is a way to protect you message, and to protect any Binary message, so that the receiver can detect whether or not an error has occurred in transmission. The protection comes way of the parity bit .
In mathematics the word parity is the quality of a number being either odd or even. for example, the number 12 has even parity, and the number 27 has odd parity. In computer science, the meaning changes just a little bit. When speaking of the parity of a data string , the parity is the quality of the string having an even or an odd number of 1's. Notice that if just one and only one bit in a string flips, then the parity of the string flips also.
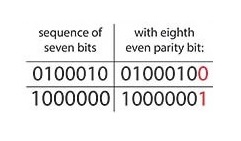
The parity bit is an extra digit that is attached to the right-most end of every string of data digits. Its function is to control the parity of the string. Because we can control the parity of a string, Computer Scientists made the decision that only strings with even parity are valid . Therefore, the parity bit's purpose is to ensure the overall parity of the data string is even. The parity bit can be either a one or a zero, whatever it needs to be, to ensure that total amount of 1's in the string is even. Notice on the right a few examples of 7-digit codes that have been protected with a parity bit.
Well, then, why don't we protect our time of day codes with parity bits? For consistency, the final parity bit will always be reddish pink. In my example code "1 0101 011110", there are seven ones. To the end of all codes a parity bit will be attached to ensure the overall parity is even. (The parity bit will be attached even if the parity is already even, in which case the parity bit will be a 0.) But in my example, the parity bit must be a 1. My code now becomes "1 0101 011110 1". My code has even parity, so it is a valid message. Attach a parity bit to the right end of your own time of day code.
Practice choosing parity bits properly with the applet below:
Well, how does the parity bit help in case of an error? If there is a single bit error in a parity-protected valid code, then the erroneous code will certainly have odd parity. Think about it: Before the error, there were an even number of 1's (that was the point fo the parity bit). After the error, either a 0 has flipped to a 1 and the number of 1's has increased by one, and the new number of 1's is odd or a 1 has flipped to a 0 and the number of 1's has decreased by one, and the new number of 1's is odd. This little fact can alert us that an error has occurred: If the receiver counts the number of ones and the number of ones is odd, then an error has occurred.
Practice detecting errors with the applet below:
For a more detailed worksheet going through Parity Bits on paper, you can download this tasksheet.
Of course, knowing that an error has occurred is totally separate from knowing how to locate the error and how to correct the error. To do that, we'll need to use a few more parity bits in the next section.
In the next section, you will have the chance to learn how several parity bits can enable the receiver to locate an error.