The History of Hamming Codes
Complex communication is one of the tools, if not the tool that sets the human race apart from all other life on earth. Modern communication is becoming more and more complex every day, not only in the way we communicate but also in the ideas that we communicate. Decades ago, a complex web of interconnected computer systems called the internet was not even thought of, and decades before that a system of broadcast communications called the radio was not thought of either. Similarly, ideas and hypotheses of political and social consequence have been speedily evolving, and have emphasized the importance of rapid and accurate communication methods.
Misunderstandings in communications are common and generally unavoidable. Any person on earth has had misunderstandings with siblings, parents, children, bosses, coworkers, and potential employers. Luckily for the human race, we have the emotional and mental capabilities to rectify, clarify, and remedy the consequences of errors in communication.
Computers and machines are not immune from errors in communication, either. In modern circuit boards and memory chips, the tiny electronic pieces are very vulnerable to magnetic noise and electrical interference. They are also vulnerable to background radioactivity, which is present everywhere. Even a simple, uncharged neutron can corrupt a message or set of instructions in one single location (Normand 1).
Computers and machines are built to perform instructions and tasks exactly as communicated, which presents a large problem. How is a machine supposed to know when it has received erroneous information? When given a set of instructions alone, a machine cannot by itself recognize an error. To recognize an error in instructions, a machine must also be given additional information to look for and to identify errors. After successfully identifying an error, the machine must also be given instructions to either halt execution or to correct the error. All of these additional steps adds complexity to a machine and to its instructions, but this additional complexity can be outweighed by the increase in efficiency of the machine.
Remember that modern computers read binary instructions and binary data streams. The term "binary" indicates that each individual piece of information, called a bit, is either a one or a zero, an on or an off, a punched hole or a non-punched hole. This quirk of machine language presents a rather rudimentary but simple way of determining whether there is an error in instruction: the parity bit.
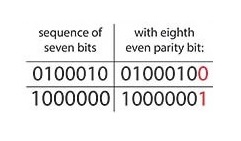
The mathematics behind a parity bit are rather simple. The word "parity" comes from the latin word "par" which means a group of two. The word "pair" in english shares this root. In mathematics, the parity of an integer is the quality of that number being either odd or even. Similarly, though not exactly the same, in computer science, the parity of a data stream or message is even if the amount of ones is even, and the parity of that stream is odd if the amount of ones is odd. Therefore, a quick consensus several decades ago in the 1930s was that each set of instructions was to have an even parity, and to ensure this, that an additional bit of information would be attached to the end of each data stream: a parity bit. This parity bit would be either a one or a zero, whichever was needed to ensure the parity of the data stream was even. On the right you can see two examples of how a parity bit ensures there is an overall even parity in the data string. (A modern application of a base-10 parity bit is found in ISBN numbers and barcodes: the very last digit of a barcode is equal to the sum of all the previous digits mod 10. (Budd, see references at the end of Part 3: The Code))

Keep in mind though, that in the 1930s computers were extremely limited in capacity and scope. The most common (though still very expensive and not common) computer in the 40s and 50s was a punched-paper computer, where information was stored on long strips of paper, with bits recorded as punched holes in the paper. A hole in the paper would signifiy a value of "1", whereas solid paper would signify a "0". On the left you can see a picture of an old punchtape.

Richard Hamming worked with punchtape computers from 1945 to 1946 in Los Alamos, managing the early computers that helped to develop the first atomic bomb. After the completion of the project, Richard Hamming moved to Bell Labs where he managed the computers and researched "computing, numerical analysis, and management of computing" (Gedda 1, see references at the end of Part 3: The Code).
The computers at Los Alamos and at Bell Labs were punch computers, but they were equipped with parity bits checks to check for errors in information. These errors were not uncommon, as brand-new programs had to be punched out by hand. So when one of these computers was given a set of instructions, the computer first examined the parity of the information to see if it was even. If the parity was even, then the computer continued with the execution of the instructions. If the parity was odd, then the computer would halt and turn on a light, indicating that there was an error in the instructions. As instructions grew more and more complex, errors also became more and more common, and the efficiency of these computers ground to a halt, as each time there was an error, the computer shut down and the paper had to be inspected manually for the error. Richard Hamming grew more and more impatient with these machines, and in an 1983 interview with Thomas Thompson described his thoughts with the words "Damn it, if the machine can detect an error, why can't it locate the position of the error and correct it?" Due to his mostly his impatience, but also the growing necessity, Richard Hamming began developing a series of error locating and correcting codes, culminating in 1950 with his paper titled "Error Detecting and Error Correcting Codes", published in Volume 29 of the Bell System Technical Journal (Gedda 1, see references at the end of Part 3: The Code). The paper provided a detailed motivation and derivation of the first Error Correcting Code, or ECC, which has since been dubbed the Hamming Code.
The most common error that appeared in the codes for Hamming were single-bit errors. Single bit errors are when a zero appears when there should be a one, or vice versa. These errors are still common now, with singular bits of data occasionally randomly flipping to the opposite of their intended value. Hamming set out to synthesize a code to protect a data stream from single bit errors, but making such a code is not an easy task. In total Hamming had to:
- Devise a way to identify whether an error has occurred (which had already been done with the parity bit, so that was easy).
- Devise a way to locate where the error occurred.
- Devise a way to include the error locating information within the data stream itself.
- Determine where in the data stream to include this addition error-locating information.
- Construct a machine or computer capable of reading the message in the data stream, interpreting correctly the error correction information included in the data stream, and executing an error fix if necessary.
(These requirements were summarized from a report by A. A. Ojiganov; see references at the end of Part 3: The Code).
At first glance to you or I, this task seems nearly impossible. How do you detect an error in a stream of data just by attaching a few more bits to it? Even if you could tell the computer that these bits have special significance, how will only a few bits suffice? How is error location and correction even possible? Hamming likely felt similar feelings at several points on his journey, but pressed on nevertheless.
The key to error location was simply an extension of parity bits. If a parity bit can detect the presence, but not the location, of an error, then perhaps more than one parity bit can help tack down the location of the error.
In the next section, you will have the chance to learn more about parity and will have the opportunity to practice using parity bits to detect errors in data strings.