Pi has been a subject of interest of many civilizations for thousands of years. Around 2000 BCE, the Babylonians approximated the value of pi to be 3.125, which they determined "by calculating the perimeter of a hexagon inscribed within a circle and assuming that the ratio of the hexagon's perimeter to the circle's circumference was 24/25" (The Editors of Encycloaedia Britannica, 2023). The Rhind papyrus indicates that the ancient Egyptians estimated the value of pi to be about 3.16045 (The Editors of Encyclopaedia Britannica, 2023). Though impressive for their time, each of these estimations only provides 2-digit accuracy.

The Egyptian Rhind Papyrus
Public domain image courtesy of Free Images
It wasn't until 250 BC that the first rigorous method for approximating pi was developed by Greek mathematician Archimedes, who used geometric approximations. Beginning with a hexagon (or a 6-gon), Archimedes inscribed and circumscribed regular polygons about a circle, then computed their perimeters to obtain upper and lower bounds for the value of pi (Borwein & Chapman, 2015). He would then double the number of sides of the polygon and repeat the process. Archimedes did this until he reached a 96-gon and determined that \(3\frac{10}{71} < \pi < 3\frac{10}{70}\) (Borwein & Chapman, 2015). That is, \(3.14085 < \pi < 3.14286\). In developing this method, Archimedes calculated pi to 3 digits of accuracy while also providing for analysis of error, which no other civilizations had taken into consideration in their calculations. Furthermore, Archimedes proved the familiar formula \(A = \pi r^2\), a formula which is now taught to children in middle school math classes all around the world (The Editors of Encyclopaedia Britannica, 2023).

The Greek mathematician Archimedes
Public domain image courtesy of Free Images
For many centuries after Archimedes' discoveries, mathematicians could continue to discover more digits of accuracy of pi only by performing extensive calculations. In 150 AD, a Greek-Roman scientist by the name of Ptolemy used Archimedes' method and took it a few steps further, approximating its value as 3.1416 (Ye, 2016). Then there was Chinese mathematician and astronomer Zu Chongzhi, who used methods similar to those of Archimedes to obtain an approximation of \(355/113 = 3.1415929\) (Zhao, 2022). Little is known about the specifics of his methods as his book was lost, but it is speculated that to achieve this level of accuracy, he would have had to begin "with a regular polygon with 24,576 sides inscribed inside a circle and perform[ed] lengthy calculations involving hundreds of square roots carried out to nine decimal places" (Zhao, 2022).
In more recent decades, growth in analytical techniques has allowed for the calculation of the value of pi using infinite series. In 1656, "while calculating an integral in an attempt to find the area of a circle with a radius of one," English mathematician John Wallis "established a formula involving the multiplication of an infinite series of fractions that was based on the value of one-half of pi" (Zhao, 2022). During that same century, Sir Isaac Newton calculated the value of pi to 16 digits of accuracy through his binomial theorem (Zhao, 2022). Later, the Gregory-Leibniz formula was developed, which states that \(\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \ldots\) (Borwein & Chapman, 2015). Using these methods of calculations, pi was able to be calculated to a much higher level of accuracy and without the same amount of tedious calculations that the geometric-based methods required.
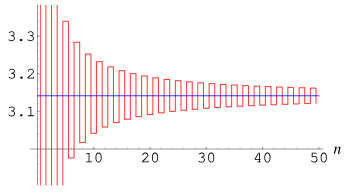
The above graph shows how the sum of the Gregory-Leibniz Series converges to pi when multiplied by 4
Image courtesy of Wolfram MathWorld
Other mathematicians chose to focus on investigating other aspects of pi, not simply its approximations. In 1761, Swiss mathematician Johann Heinrich Lambert proved that pi is an irrational number, meaning that "it has an infinite number of digits that never enter a repeating pattern" (Ye, 2016). German mathematician Ferdinand von Lindemann proved in 1882 that pi is not a transcendental number, meaning that it "cannot be expressed in a rational algebraic equation" (Ye, 2016). In the midst of all these proofs and the development of infinite series, a man named William Jones introduced the use of the Greek letter \(\pi\) as a representation of pi in the year 1706, which was later made popular by Leonhard Euler (Zhao, 2022).

William Jones introduced the use of the Greek letter \(\pi\) to represent pi
Public domain image courtesy of Free Images
Some of the most recent progress in calculating pi took place in the early 1900s. Indian mathematician Srinivasa Ramanujan "developed an incredibly efficient formula for calculating pi based on its reciprocal fraction, which was later incorporated into computer algorithms" (Zhao, 2022). His formula, which is rather complicated but extremely accurate, can be seen below: \[\frac{1}{\pi} = 2\sqrt{2} / 9801 \sum_{k=0}^{\infty} \frac{(4k)!(1103 + 26390k)}{(k!)^4 396^{4k}}\] (Borwein & Chapman, 2015).

Indian Mathematician Srinivasa Ramanujan (center)
Public domain image courtesy of Free Images