Project Navigation
Significance & Applications
One of the reasons pi is so significant is because, as it is so closely tied to circles, it is an essential element in calculating the area of a circle as well as calculating areas and volumes of circular objects. We know pi, by definition, is the ratio of the circumference of any circle to its diameter. Thus, \(C=\pi D=2\pi r\). Now, recall that we know the area of a rectangle to be \(A=\text{length} \times \text{width}\). If we were to divide our circle into triangular segments, these segments could be rearranged to form a rectangle with a length of \(\pi r\) and a height of \(r\) (Dhakal, n.d.). Thus, we can calculate the area of the circle by calculating the area of the resulting rectangle. That is, \(A=(\pi r)(r)=\pi r^2\) (Dhakal, n.d.). The more slices the circle is broken into, the easier this is to visualize (Dhakal, n.d.). Because pi is integral to understanding the dimensions and areas of circles, it is also necessary to understand and calculate measures such as surface area and volume of 3D objects which contain circles, such as spheres, cones, and cylinders.
Check out how to discover the formula for the area of a circle below!
Instructions: Use the left slider to adjust the number of slices dividing the circle. Use the right slider to unfold the circle.
Use the vertical slider to move the slices of the circle to create a rectangle. What is the area of the rectangle? What does this tell you about the area of the circle?
Applet by Bed Prasad Dhakal found on Geogebra
Another reason pi is so significant is because of its use in converting degrees to radians. But wait? Why is converting to radians even useful if degrees are already understood? Degrees are a human constructed system (Khan Academy, 2012). There are a few theories as to where the notion of using 360 to describe a full rotation came from. Ancient calendars were based on 360 days in a year, astronomers observed that celestial objects moved about 1/360th of the sky each day, the ancient Babylonians had a base 60 number system, and the list goes on (Khan Academy, 2012). Radians on the other hand have a much more pure, mathematical foundation. One radian is the measure of an angle at the center of a circle whose arc has the same length as the radius of the circle (Khan Academy, 2012). Knowing this and the fact that the measure of the circumference of a circle is \(2\pi r\), we may say that there are \(2\pi\) radians in a circle, just as we would say there are 360 degrees in a circle (Khan Academy, 2012). This further means that \(\pi\) radians is equal to 180 degrees, thus we can use the conversion factor \(1 \text{ radian} = \frac{180}{\pi} \text{ degrees}\) to convert between the two (Khan Academy, 2012). As radians are a more universal form of measurement, they are used a lot more frequently within the math classroom as well as within many different math-related professions.
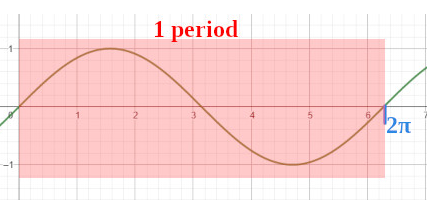
Finally, pi is significant because of the role it plays in understanding sinusoidal functions. When studying such functions, we use the term "period" to describe the length of a complete cycle,
which for a typical sinusoid, is \(2\pi\) (Frequency and Period of Sinusoidal Functions, 2023). This makes sense as a circle also completes one full rotation in \(2\pi\) radians,
and the points comprising the sine wave can be determined using the unit circle. However, most waves are typically stretched or compacted, thus, we use the term "frequency" to describe the number
of cycles that occur in \(2\pi\). Thus, the period of any sinusoidal function can then be found using the following equation: \(period = \frac{2\pi}{\text{frequency}}\)
(Frequency and Period of Sinusoidal Functions, 2023).
It's now clear that pi is necessary to find certain volumes and surface areas, to use radians as a form of measurement, or study sinusoidal functions, but does any of this have any actual
"real world" impact? The answer is actually yes! Engineering is one of many fields that makes use of this mathematical constant in order to make important calculations every day. Anita Sengupta,
an engineer who works at NASA's Jet Propulsion Lab (JPL), noted, "Pi has allowed me to calculate the size of a shield needed to enter the atmosphere of Venus and the size of a parachute that could
safely land the Curiosity rover on the surface of Mars"(Holecko, 2023). Other NASA scientists have utilized pi to do such things as: calculate the length of time it takes a spacecraft to orbit the dwarf
planet Ceres at any given altitude, determine how much hydrogen might be available for chemical processes in the ocean beneath the surface of Europa (which is one of Jupiter's moons), and calculate distance
between stars (Jet Propulsion Laboratory, 2015). All of these calculations require the use of pi as they either involve understanding the geometry of a sphere or the movement of objects in a circular motion.

Pi also plays a crucial role in the study of waves, due to its involvement in the calculation of wave periods. Waves are a part of many aspects of life, from methods of communication like talking on the phone,
watching TV, and listening to the radio, to medical applications such as ultrasound imaging (Shah, 2016). The bounce of a spring and the vibration of a string can both be described by waves (Shah, 2016). Even
many natural phenomena like light, sound, and ocean water travel in waves (Shah, 2016). In order to study naturally occurring waves or have functioning technology that relies on wave mechanics, one must have an
understanding of pi.

Pi is used in construction for such calculations as determining how much power can run through a wire with a cross-section of a specific width and determining the amount of material needed to construct
such things as bridges and arches (as these are semicircles) (Shah, 2016). Pi is used by statisticians to track population dynamics (Shah, 2016). It's used in the medical field "to accurately describe the
geometry of the DNA double helix" (Sanchez & Grant, 2015). It's even been used to study the shape of the eye, which is spherical, which has helped make a lot of advancements in the areas of optometry and
ophthalmology (Sanchez & Grant, 2015). And these are all only a small sample of the ways pi is utilized in the modern day. Pi may be mysterious and abstract, but it has many practical applications in real-life.
Perhaps this is the reason it's such a central object of study. It's so essential yet so misunderstood.



