Explanation of Mathematics

What is a polynomial?

The word polynomial means "many names or terms" (Weisstein, 2002). Polynomials (of one variable) have the following form: \(a_{n}x^{n}+...+a_{2}x^{2}+a_{1}x+a_{0}\).

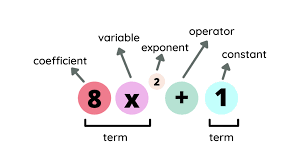
Classification of Polynomials

Polynomials are classified and organized by their degre or order, this is determined by the hightest power (Weisstein, 2002). For example, the polynomial expression \(8x^{7}+3x^{4}-2x\) has a degree 7. Polynomials of degree 1 are linear, and polynomials of degree 2 are quadratics. These are the most well known kinds of polynomials (Wildberger, 2011).

Solving Polynomial Equations

Polynomials with higher degrees are more difficult to factor and find its roots. Take note that there are different ways to solve a polynomial, and while the stes may be similar for a lot, not every polynomial can be solved the same way.

Polynomial Equations of Degree 1

Polynomials of degree one can be solved by islolating the variable. We can do this through algebraic manipulation of the original equation.

Examples

\(5x+2=0\)

This example only takes two steps to solve for \(x\). Subtract 2 on both sides, this will leave you with \(5x=-2\); then divide by 5 on both sides. The solution is \(x=-\frac{2}{5}\).

\(\frac{3y}{4}+5=15\)

Subtract 5 from both sides; \(\frac{3y}{4}=10\),

Multiply both sides by 4; \(3w=40\)

Divide both sides by 3, which gives you the solution \(\frac{40}{3}\)

Polynomial Equations of Degree 2 (Quadratics)

There are three ways to solve quadratic equations: factoring, completing the square, and using the quadratic formula.

Factoring

Polynomial equations of degree two are made of factors; they have two zeros/roots (by the Fundamental Theorem of Algebra), so there are two factors for each quadratic equation (Burton, 2006). By factoring, the polynomial is broken down into these factors (Weisstein, 2002). This can be done by finding two numbers whose sum is \(b\) and whose product is \(ac\) for a polynomial equation of the form: \(ax^{2}+bx+c=0\) (Brown, 2020).

\(x^{2}+2x=15\)

Step 1: Make sure the polynomial equation is in the form: \(ax^{2}+bx+c=0\). For our example, we need to subtract 15 on both sides,

\(x^{2}+2x-15=0\)

Step 2: Find two numbers whose sum is equal to \(b\) and whose product is \(ac\). Let's look at the example given:

\(x^{2}+2x=15\) \(a=1\),\(b=2\), and \(ac=-15\)

You may find listing the factors of \(ac\) to be helpful. Let's list the factors of -15.

-15, -5, -3, -1, 1, 3, 5, 15.

Putting these factors in a table will also help visualize their sum/difference. You may notice that 5 and -3 add to give 2 and multiply -15.

Step 3: Break down the polynomial. For quadratic equations, the factors will have the form : \((x-h)(x-g)=0\). Here \(h\) and \(g\) are replaced by the factors of \(ac\) that we just found. In this specific example, those are 5 and -3. Here is the factored polynomial:

\((x-5)(x+3)=0\)

Take note that the sign changes because \(x--3=x+3\). Be aware of your signs, you can make a small mistake by not changing your sign and get a totally different solution. If you want to make sure that the polynomial is correctly factored, you may FOIL or expand the factored equation, giving you the original polynomial.

Step 4: Now that the polynomial is factored it is easy to find the \(x\) values that will give 0. Set each individual factor to zero.

\((x-5)=0\), \(x=5\)

\((x-3)=0\), \(x=3\)

5 and 3 are the solutions to this polynomial equation. These are referred to as zeros. When these values of \(x\) are plugged in, the equation will equal zero. On a graph, this corresponds to where the polynomial function intercepts the \(x\) axis.

Completing the Square

The name for this method comes from the geometrical connection it has. When one uses this method they are quite literally completing the square (Hughes).

Let's look at the example \(x^{2}+6x-7=0\).

Step 1: Put the polynomial equation into the form \(ax^{2}+bx=c\) by adding 7 to both sides of the equation resulting in

\(x^{2}+6x=7\)

Step 2: \(b=6\), so plug that into (\(\frac{1}{2}b)^{2}\) Giving us

(\(\frac{1}{2}6)^{2}=3^{2}=9\)

Add 9 to both sides of the equation:

\(x^{2}+6x+9=7+9\)

Step 3: Notice that the left side of the equation can simplify to \((x+12b)2\). Recall that \(b=6\), so we have

\((x+\frac{1}{2}6)^{2}\)

And our equation becomes

\((x+3)^{2}=16\)

Step 4: Solve for the \(x\) variable

\((x+3)^{2}=16\)

\(\sqrt{(x=3)^{2}}=\pm{16}\) \((x+3)=\pm{4}\)

At this part of step 4, we have \(\pm\sqrt{16}\). This is because \(\sqrt{16}\) results in two answer; both \(4^{2}\) and \(-4^{2}\) equals 16. Keep this in mind because quadratic equations each have two roots. Continuing with the example, there are two equations to solve: (\x+3=4\) and \(x+3=-4\). Resulting in \(x=1\) and \(x=-7\)

For a more thorough explanation watch this video: Completing the Square.

Quadratic Formula

This method will work for any quadratic equation. A polynomial equation of degree two with general coefficients is \(ax^{2}+bx+c=0\). The quadratic formula is derived from completing the sqaure with general coefficients (Weisstein, 2002). This applet is a great resource to use in seeing how the quadratic formula is derived.

See if you can derive the formula yourself. Start out with the equation \(ax^{2}+bx+c=0\). We want the equation to be of the form: \(ax^{2}+bx=c\).

If you've derived it correctly, you should get

\(x=-b \pm\sqrt{\frac{b^{2}-4ac}{2a}}\)

To use this formula, ensure that the polynomial is in the form \(ax^{2}+bx+c=0\). Then, the values for \(a,b,c\) are inputed and you can go from there. This results in two roots of the polynomial equation.

Watch this video for further explanation.

Polynomial Equation of Degree 3 and Above

Polynomial equation of degree 3 and above are more difficult to solve. However, for degrees 3 and 4, there existis The Cubic Formula and The Quartic Formula. If you do want to venture into solving polynomials with higher degrees, the best strategy is breaking them donw into polynomials of smaller degrees by pulling out common factors. Doing it in smaller parts makes it more managable and then you can use methods that are more familiar (Brown, 2020).

Take the polynomial function \(f(x)=x^3-4x^2-3x+12\). Group the first two terms together and the last two terms together:

\(f(x)=(x^3-4x^2)-(3x-12)\) Then pull out common factors. The first group has an \(x2\) in common and the second group has a 3 in common. Pulling these out leaves: \(f(x)=x^2(x-4)-3(x-4)\) Notice that we have \((x-4)\) in each group now. Simplifying this leaves: \(f(x)=(x-4)^2(x^2-3)\). Now there is a factor and a degree two polynomial. Set the factor equal to zero: \((x-4)^2=0\) Taking the square root of both sides results in \(x-4=0\) Adding 4 to both sides then results in \(x=4\) Next, we solve for \(x\) for the degree 2 polynomial so set : \(x^2-3=0\). Add three to both sides: \(x^2=3\). Take the square root of both sides and the result is: \(x=3\). These are the other two solutions (so we have found all three solutions). Alternatively, the quadratic formula can be used to find the roots of the quadratic (UCSB, 2016). \(x^2-3=0\) is in the form \(ax^2+bx+c=0\) so we can plug in our values. \(a=1\), \(b=0\), \(c=-3\). So we have \(x=\frac{-(0)\pm\sqrt{(0)^2-4(-3)(1)}} {2(1)}= \frac{\pm\sqrt{12}}{2}=\frac{\pm2\sqrt{3}}{2}=\pm\sqrt{3}\).

Graphs of Polynomials

Not only can we look at polynomials algebraically, but we can also see a representation of it on a graph. Graphs behave differently at various x-intercepts. Depending on the function, the graph will cross over the x-axis t the intercept, or it will touch the x-axis and then bounce off.

The figure above is a graph of the function \(f(x)=(x+3)(x-2)^{2}(x+1)^{3}\). The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. For zeros with even multiplicities, the graphs touch (or are tangent) to the x-axis at these x-values. For zeros with odd multiplicity, the graphs cross (or intersect) the x-axis. Below is figure of some examples.