3 Explanation of Mathematics
3.1 Definitions
This section begins with a list of deffinitions, given to review some fundamentals of Number Theory. Many of these fundamentals are widely taught in both primary and secondary education. Although this list seems tedious, these precise deffinitions are foundational to the mathematics in later sections.
An integer \( n\) is either a positive or negative whole number or zero. The set of integers, denoted as \(\mathbb{Z}\), is the collection of positive and negative whole numbers and zero, ie \( \{... -3, -2, -1, 0, 1, 2, 3 \: ... \} \). Number Theory focuses on the set of positive integers, denoted \(\mathbb{Z}^+ \).
Let \( m, n\) be integers. \( m\) is a divisor of \(n\) , denoted \(m | n\) , if and only if m > 0 and \(n = mk \) for some integer \(k\) . Alternatively, \(m\) divides \(n\) or \(m\) is a factor of \(n\) if \( \frac{m}{n} \) is an integer.
A positive integer \( p\) greater than 1 is prime if and only if its only divisors are 1 and itself. The famous Greek philosopher Euclid proved there are an infinite number of primes (Caldwell, 2021). This deffinition of prime excludes 1 and negative numbers.
The prime factorization of an integer \( n\) is the list of prime numbers when multiplied together creates \( n\). Prime numbers can be repeated in a prime factorization, which is denoted as a prime to a power. The Fundamental Theorem of Arithmetic states that every integer greater than 1 has a unique prime factorization (Weisstein, 2022).
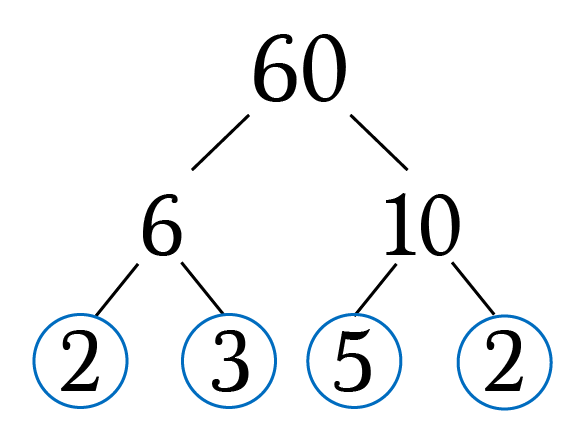
Prime Factorization Trees, as shown above, are very helpful in finding a number's Prime Factorization.
Click here to learn more
The greatest common divisor of integers \( m, n\), denoted \( \gcd(m,n)\), is the largest integer \( g\) for which \( g|m\) and \( g|nn\). In the United Kingdom, the GCD is referred to as the Highest Common Factor or HCF ("Prime factors", 2022).
Two integers, \( m, n\) are relatively prime, denoted \( m \perp n\) if and only if their greatest common factor is 1, or \(\gcd(m,n) = 1\).
The following comes from the above deffinitions:
- 5 is an integer while 12 is not
- 4 divides 8 since \(8 = 4k \) where \(k = 2 \)
- The numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, etc are prime, whereas all even numbers excluding two are not prime but composite (since two divides every even number).
- The prime factorization of 24 is found by observing \(24 = 6 \cdot 4\) and \( 6 = 3 \cdot 2\) and \(4 = 2 \cdot 2\), so \(24 = (3 \cdot 2) \cdot (2 \cdot 2) = 2^3 \cdot 3\)
- The greatest common divisor is found by finding all divisors (also known as factors) of the two numbers, then their common divisors, and selecting which is the largest (or by utilizing the Euclidean Algorithm, as described by Lynn, n.d.). For example, \(\gcd(40, 25)\)is found by observing the factors of 40 and 25, which are \(40 = 1 \cdot 40 = 2 \cdot 20 = 4 \cdot 10 = 4 \cdot 8\) and and \(25 = 1 \cdot 25 = 5 \cdot 5\). The factors in common between the two are 5 and 1, so 5 is the greatest common divisor of 25 and 40.
- Notably, the numbers 4 and 9 are relatively prime, despite not being prime themselves, since their greatest common divisor is 1.
3.2 Modular Arithmetic
Watch this video for an introduction to how modular arithmetic works!
Carl Friedrich Gauss invented Modular Arithmetic in the early 1800s (Taylor, 2012). At its core, Modular Arithmetic provides a much easier way to work with extremely large numbers. "Clock Arithmetic" is one analogy for Modular Arithmetic where numbers on the clock are equivalence classes and any integer can be written as one of these equivalence classes (more on this later). The Division Algorithm is crucial to understanding Modular Arithmetic:
Let \(m,n\) be integers and \(n \neq 0\). Then there exists unique integers, \(q\) and \(r\), such that \(m = nq + r \) where \( 0 \leq r < |n| \).
In the Division Algorithm, the number \(m\) is the dividend, \(n\) is the divisor, \(q\) is the quotient and \(r\) is the remainder. Typically in division, the quotient is emphasized, such as "45 divided by 8 equals 5" where 45 is the dividend, 8 is the divisor and 5 is the quotient. In Modular Arithmetic, the focus is on the remainder with \(m \!\! \mod n = r\).
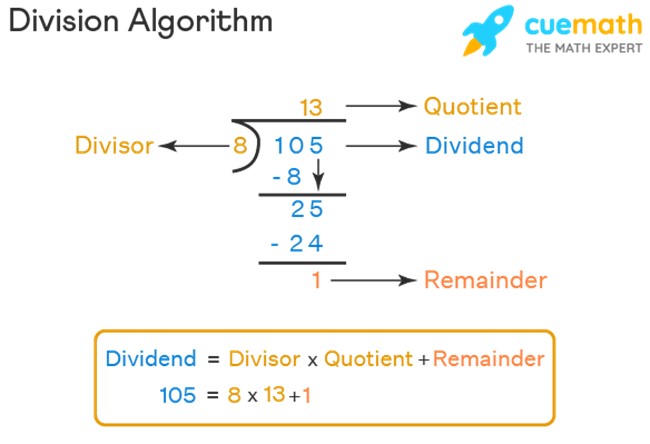
From CueMath.com, see Further Readings for source details
In the above expression, 8 is the divisor, 105 is the dividend, 13 is the quotient, and 1 is the remainder. In the format of the Division Algorithm, this becomes \(105 = 8 \cdot 13 + 1\). Modular Arithmetic focuses on the remainder, so \(105 \!\! \mod 8 = 1\), since 1 is the remainder.
By the constraint of \(0 < r \leq |n|\) in the Division Algorithm, the remainder is always a value from 0 to \(n-1\). Thus, by using Modular Arithmetic, for \(a \!\! \mod n\), any integer \(a\) can be represented as one of \(n\) equivalence classes where each equivalence class is a number ranging from 0 to \(n-1\). This creates a sort of "clock", where \(r\) is the current time and the number of rotations (\(q\)) is irrelevant.

Illustration from Bernard Darnton's website, see Further Readings for source details
The above illustration displays how numbers are on a clock face create the equivaence classes of Modular Arithmetic; since 14 o'clock is equivalent to 2 o'clock, they are in the same equivalence class.
$$0 \!\! \mod 5 = 0 \quad \quad 1 \!\! \mod 5 = 1 \quad \quad 2 \!\! \mod 5 = 2 \quad \quad 3 \!\! \mod 5 = 3 \quad \quad 4 \!\! \mod 5= 4$$ $$5 \!\! \mod 5 = 0 \quad \quad 6 \!\! \mod 5 = 1 \quad \quad 7 \!\! \mod 5= 2 \quad \quad 8 \!\! \mod 5= 3 \quad \quad 9 \!\! \mod 5 = 4$$ As one can observe, this creates a clock face with five values: 0, 1, 2, 3, and 4.
Any number, no matter how large, can be represented as one of five equivalence classes. For example 758943 in \(\!\! \mod 5\) is simply 3.
3.3 Theorems
The following exploration of these theorems are crucial to understanding why the RSA Cryptographic System works. The first of such theorems is called Fermat's Little Theorem after Pierre de Fermat (not to be confused with Fermat's Last Theorem, which was an open problem for 300 years until being proved by Andrew Wiles as discussed by Harris (2019). The proofs for all three of the following theorems is found in Hungerford (2012).
If \(a\) is an integer, \(p\) is prime and \(p\) does not divide \(a\), then \(a^{p-1} \equiv 1 \!\! \mod p\)
Let \(p, r, s, c\) be integers and \(p\) prime. If \(p\) does not divide \(c\) and \(rc \equiv sc \!\!\mod p\), then \(r \equiv s \!\! \mod p\).
Let \(p\) and \(q\) be distinct positive primes. Let \(n = pq\) and \(k = (p-1)(q-1).\) Choose \(d\) such that \(\gcd(d, k) = 1\). Furthermore, let \(e\) be an integer such that \(de \equiv 1 \!\! \mod k\). Then \(b^{ed} \equiv b \!\! \mod n\) for every integer \(b\).
Fermat's Little Theorem is relatively simple in it's approach, for any integer \(a\) and prime \(p\) where \(p\) does not divide \(a\), then \(a^{p-1}\) is congruent to 1 in \(\! \! \mod p\). So, without the need for calculating \(2^{42}\), Fermat's Little Theorem reveals \(2^{43-1} \equiv 1 \!\! \mod 43\).
Similarly, Lemma 2 shows a simplification with Modular Arithmetic. For an example with small integers, begin with \(34 \equiv 8 \! \! \mod 13\). It follows that \(17 \cdot 2 \equiv 4 \cdot 2 \! \! \mod 13\). Since 13 does not divide 2, then it follows \(17 \equiv 4 \! \! \mod 13\). This is useful for simplifying extremely large numbers with Modular Arithmetic.
The significance of Theorem 3 will be discussed in the next section about Number Theory's application in the RSA cyrptosystem. In Hungerford's proof of Theorem 3, Fermat's Little Theorem and Lemma 2 are used.