2 History and Background
2.1 Caesar Cipher
One of the earlier forms of cryptography is the Caesar Cipher. Of course, this encryption method is named after Julius Caesar, who was said to use this shift cipher for military correspondence ("Cracking the Code", 2019). Unfortunately, this simple cipher is easily cracked, but still showcases some cryptography fundamentals.
Cryptography algorithms begin with taking a message of plain text, such as "This is secret" and translating it into numbers. For this example, a space is 00, A is 01, B is 02, and so forth with Z being 26. The message "This is secret" becomes
| T | H | I | S | I | S | S | E | C | R | E | T | plain text | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 08 | 09 | 19 | 00 | 09 | 19 | 00 | 19 | 05 | 03 | 18 | 05 | 20 | numeric plain text |
Next, the Caesar Cipher encrypts the plain text into cipher text by shifting all the numbers by the same amount. For this example, the shift is 3 (rumored to be Caesar's favorite shift).
| T | H | I | S | I | S | S | E | C | R | E | T | plain text | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 08 | 09 | 19 | 00 | 09 | 19 | 00 | 19 | 05 | 03 | 18 | 05 | 20 | numeric plain text |
| 23 | 11 | 12 | 22 | 03 | 12 | 22 | 03 | 22 | 08 | 06 | 21 | 08 | 23 | cipher text (from shifting 3) |
| W | K | L | V | C | L | V | C | V | H | F | U | H | W | alphabetic cipher text |
The cipher text, WKLVCLVCVHFUHW, can be decrypted by using a reverse shift of 3 and becomes our plain text "This is secret." Of course, the Caesar Cipher can be hacked by testing various shifts until a coherent message is found ("Cracking the Code", 2019).
2.2 Vigenere Cipher
The Vigenere Cipher is a type of modified Caesar Cipher that was invented by the Italian cryptologist Giovan Battista Bellaso in the 15th century (Norman, 2022).
The main difference between the Vigenere Cipher and Caesar Cipher is the Vigenere requires a key word that is repeated until it reaches the length of the plain text. Each letter of the key word determines a separate Caesar Cipher shift; so if a key word began with the letters "E" and "V", then the first letter in plain text would be shifted down 5 and the second letter would be shifted down 22. This is where Modular Arithmetic, as discussed in 3.2, the Mathematics Section. would become necessary. Encrypting with a Vigenere Cipher would quickly become cumbersome with large numbers since it would be difficult to determine what letter the number 47 corresponds to. With Modular Arithmetic, the equivalence statement 47 mod 27 = 20 (26 letters and a space) would help determine 47 corresponds to T and thus translate the cipher text into letters.
Returning to the previous example of the code message "This is secret", a Vigenere Cipher with a key word "lemon" would encrypt the message using the following individual Cesar shifts shown below.
| T | H | I | S | I | S | S | E | C | R | E | T | plain text | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 08 | 09 | 19 | 00 | 09 | 19 | 00 | 19 | 05 | 03 | 18 | 05 | 20 | numeric plain text |
| L | E | M | O | N | L | E | M | O | N | L | E | M | O | key word |
| 12 | 05 | 13 | 15 | 14 | 12 | 05 | 13 | 15 | 14 | 12 | 05 | 13 | 15 | key shifts |
Notice that the message contains 14 characters, with two of them being spaces, so the key was repeated almost three times. Next, the plain text numbers are shifted according to their individual shift, so T = 20 is shifted L = 12, becoming 32 mod 27 = 5 = E in cipher text.
| T | H | I | S | I | S | S | E | C | R | E | T | plain text | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 08 | 09 | 19 | 00 | 09 | 19 | 00 | 19 | 05 | 03 | 18 | 05 | 20 | numeric plain text |
| 12 | 05 | 13 | 15 | 14 | 12 | 05 | 13 | 15 | 14 | 12 | 05 | 13 | 15 | key shifts (from lemon) |
| 32 | 13 | 22 | 34 | 14 | 21 | 24 | 13 | 34 | 19 | 15 | 23 | 18 | 25 | cipher text (from adding key shifts) |
| 05 | 13 | 22 | 07 | 14 | 21 | 24 | 13 | 07 | 19 | 15 | 23 | 18 | 25 | cipher text (mod 27 for letters) |
| E | M | V | G | N | U | X | M | G | S | O | W | R | Y | alphabetic cipher text |
The method for decryption also requires the key word and is similar to encryption, only the shifts from the key are subtracted rather than added to obtain the original message in plain text. Unfortunately, although this cryptography method was secure and unbreakable for over hundred years, Friedrich Kasiski and Charles Babbage independently published a methods for breaking the Vigenere Cipher in the 19th century (Norman, 2022). Modern computers have made cracking this code even easier using techniques like frequency analysis, which utilizes facts such as e being the most commonly occurring letter.
Interestingly, the Confederate Army used the Vigenere Cipher during the Civil War and the Union regularly cracked the Confederacy's messages.
2.3 Public Key Cryptography
Modern cryptography has become increasingly more important as the need for encryption has increased. In the Caesar and Vigenere Cipher, the key to the cipher was given beforehand, probably in person for most cases. In the digital age, where encryption is needed for anything from ATM pins to passwords and online payments, it's infeasible to meet in person and determine a key to encode sensitive messages sent over the internet. Furthermore, it would be very expensive and tedious for a company to maintain a database of private personalized keys for every customer. Public Key Cryptography is the solution to both of these problems and rises to the need for secure encryption across the internet.
The basic idea of Public Key Cryptography relies upon the ideal that the key for encryption is public, but the key for decryption is secret. To send encrypted data to a specific person, the sender must encrypt their data with the recipient's public key, and the recipient must decrypt the message with their corresponding private key ("Public Key Cryptography", 2021). Below is a figure from IBM showing a simplified flow chart of this cryptography system.
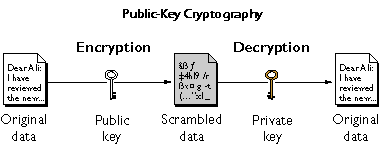
Flow chart of Public Key Cryptograph ("Public Key Cryptography", 2021)
The RSA Cryptosystem, one of the oldest public key cryptosystems, was invented in 1977 by three students at Massachusetts Institute of Technology: Ron Rivest, Adi Shamir and Leonard Adleman. This system is relies on the difficulty of factoring the product of two large prime numbers (large as in 1024 and 2048 bits according to IBM). The intricacies of the RSA system rely upon elementary Number Theory discussed in the Mathematics Section and their application will be explored in the The RSA Cryptosystem Section.