Spirals: History

Archimedean/Arithmatic

Archimedes is a greek mathematician, engineer, astronomer, and inventor. Archimedes is considered to be one of the greatest mathematicians of ancient history, leading the discoveries of pi, calculus, and the process of rigorous proof analysis. Not only was he the first to apply mathematics to the scientific study of physics, but he also used mathematics when studying the measurements of the Earth, Sun, and Moon (Wikipedia,2022).

Archimedes, the talented man he is, discovered the first mathematical spiral recorded in history. This is known as, you guessed it, the Archimedes Spiral. He first discovered the spiral around 225 BC and recorded his discoveries in a memorandum which he titled On Spirals. His discovery happened by chance when he was fiddling with a compass. While rotating clockwise around a fixed point Archimedes pulled one of the compass legs out at a steady rate.


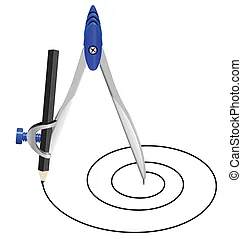
He discovered that while the spiral kept a constant distance between each revolution, the magnitude at which the spiral moved matched the magnitude of the rotating compass. He went on to define this spiral as "the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity."

Archimedes also further describes the spiral as squaring the circle and trisecting the angle. This will require the use of Polar Coordinates to understand, which will be described later in the site.

Equiangular/Logarithmic

The logarithmic, or equiangular, spiral has many contributors to its discoveries so we will dive into a few. The first to describe the spiral, Albrecht Durer (pictured below), called it the eternal line in 1525.

However, it wasn't until 1638 that the spiral really gained traction in the mathematical world by Rene Descartes (left) and Jacob Bernoulli (right) who described the spiral as the "marvelous spiral". Rene Descartes is a revered philosopher and mathematician who became interested in spirals during his study of dynamics ("Equiangular Spiral",2022).

Descartes said that both the "uniform rectilinear motion of a point along a segment, and the uniform circular motion of the segment around a point" must simultaneously be considered in order for the moving point's path to describe the spiral. The Logarithmic spiral was officially defined as "a spiral for which the radius grows exponentially with the angle" or "distances where a radius from the origin meets the curve are in geometric progression".

Later Descartes argued that when it came to spirals more needed to be explored, this led to further study by Jacob Bernoulli who was so fascinated by the spiral that he had it engraved on his headstone. This depiction of the spiral is accompanied by a quote which reads Eadem mutato resurgo : 'Although changed, I rise again the same'. But by mistake, Bernoulli's mason engraved the wrong type of spiral, an Archimedian spiral, instead.



Bernoulli was particularly fascinated with the Golden/Fibonacci Spiral which is an extension of the Logarithmic spiral. More information can be discovered about this spiral here.

Fermat's/Parabolic

Contrasting the Archimedian and Logarithmic Spiral, the Fermat's, or Parabolic, Spiral displays the distance between turns growing inversely proportionately to their distance from the spiral center. The Parabolic spiral was discovered by French mathematician Pierre Fermat in 1636 and was subseuently named after him. Fermat spent most of his career pioneering analytic geometry, analyzing number theory and previously received a bachelor in civil law in 1626 ("Fermat's spiral",2019).

He chose to look back and study the work of Archimedes which led him to study spirals. Although not much is known about his discovery of the Parabolic spiral, while examining a separate spiral, the phyllotaxis spiral, he noticed that when all the elements are the same size, the shape of the spirals is that of a Parabolic spiral's. Fermat went on to officially define this spiral as "a plane curve with the property that the area between any two consecutive full turns around the spiral remains unchanged".

Polar Coordinates

Now, none of these spirals will make any sense without background knowledge of polar coordinates. Polar Coordinates are "a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction".

Although it is disputed who first introduced the polar coordinate system it is suggested that Gregoire de Saint-Vincent (left) and Bonaventura Cavalieri (middle) introduced the concept around the same time. Saint-Vincent wrote about them in 1652 publishing his findings in 1647 while Cavalieri published his findings in 1625 with corrections in 1647.

Despite thier discoveries, Sir Isaac Newton (right) was the first to employ them as a means of locating a point on a plane. Without this coordinate system, plotting spirals mathematically becomes difficult.