Explanation of Mathematics
What is Pascal's triangle? Saucedo states "Pascal's triangle is an infinite array of numbers which is constructed by beginning with the number 1" (2019). Rows are counted beginning with the first "1" being row zero, and entries are counted within each row starting from the left at zero. In the following figure, the circled 4 would be entry two in row four.
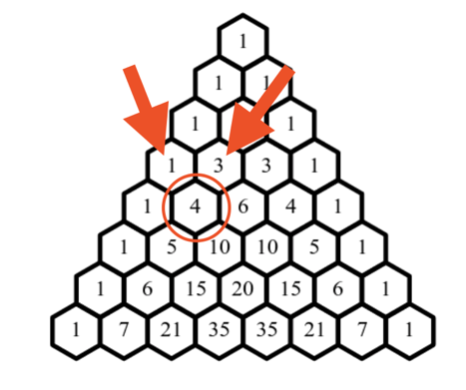
Pascal's triangle holds five properties that help to define it. Each of them can be proven, and the proofs can be seen in Kuhlmann's thesis.
- "Every row starts and terminates with 1
- Every row is symmetric about its center, and thus the triangle as a whole is symmetric about the vertical line running through its center.
- The sum of the numbers on any row \(n\) is \(2^n\)
- The sum of the rows 0 through \(m\) is \(2^{m+1}-1\)
- Every entry in each row is the sum of the numbers to its left and right on the previous row." (Kuhlmann, 2013)
As property 5 states, each entry is obtained by summing the numbers directly above it. So, the circled 4 in the previous figure was the result of adding the 1 and 3 above it. When numbers are summed, the triangle can be expanded to an infinite number of rows.
Each entry can also be obtained by computing a combination. What is a combination? Davidson describes a combination as "When of many things we may choose a certain number, all the ways of taking as many as we are allowed out of all those offered to our choice are here called the 'different combinations'" (1988). Typically, a combination is represented as \({n \choose r}\) where \(n\) is the total number of objects or options and \(r\) is the amount we want to select. A combination is a selection of things when the order of the things selected is not important. For example, if we wanted to know how many options there were for a 3 digit passcode, we would not want to represent this as a set of combinations because "123" is a different passcode than "132". But, if we wanted to know which three students selected out of a class could participate in an activity then combinations would be applicable if it did not matter what order the students were selected in. The number of combinations is calculated by the formula \({n \choose r} = \frac{n!}{r!(n-r)!}\) or by the nCr function that is available on many calculators.
Now that we have learned about calculating combinations, how exactly do they relate to Pascal's triangle? Each entry can be calculated using combinations! In each combination \(n\) represents the row number and \(r\) represents the entry number. A filled in triangle built with combinations is shown in the next figure.

Representing the triangle as combinations is helpful when you are given a problem that requires use of combinations. Suppose you need to compute \({15 \choose 3}\). This would be tedious by hand and the answer is not obvious. To find the solution you simply need to go to the fifteenth row and find entry three. As a general rule, "the number of ways to select a set of \(n\) elements from a set of \(m\) distinct elements is given by the intersection of row \(m\) and diagonal \(n\)" (Smith, 1973).