Fractals are patterns that begin with a geometric shape or pattern, then the pattern is repeated. The repeated pattern seems like there is not prediction; however, after multiple repeats of the pattern, the fractal become more predictable in its pattern. "Fractals are images of dynamic systems — the pictures of Chaos.1"

The Sierpinski Triangle is a pattern of a triangle with triangles inside. The Sierpinski Triangle is a decorative pattern used in architecture and mosaic tiles.2 It is a self-similar fractal, which means the more you zoom in, the image will copy itself.
Sierpinski's triangle ties closely with Pascal's Traingle. Below is the link to an applet that displays and shows how Pascla's Triangle works:
The link below contains a link to a game that allows the learner to better understand how Pascal's Triangle coincides with the Sierpinski triangle.
A video explaining how Pascal's Triangle is applied to the Binomial Theorem, the Sierpinski Triangle, and more!
The Mathematical Secrets of Pascal's Triangle
The Koch Snowflake begins with an equilateral triangle. Then, a repeated triangle is applied leading to a snowflake shape.

An amazing thing about the Koch snowflake is that it is continuous everywhere, but in no way differentiable.3
In the table below, the number of sides, side lengths, and perimeter of lengths for the Koch snowflae are shown. Notice how quicky the number of sides increases.
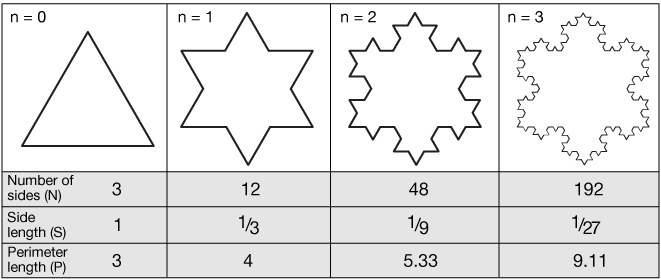
Credit: https://xaktly.com/KochSnowflake.html
Fractals are found throughout nature. Fractals are seen in plants, specifically trees, leaves, and succulents. Fractals are in Biology. Some biological examples include shells, neurons, and veins. Fractals are also found in earth including rocks, mountains, coastlines, and rivers. Water particles also create fractals as clouds are considered fractals and snowflakes are types of fractals. Other fractals in nature include lightning. Although geometric fractals tend to go on infinitely, fractals in nature generally have an ending point.
Leonardo da Vinci studied branches in trees and their patterns. He was possibly one of the first known artists and scientists to describe fractals within nature.

Leaves are considered fractals in that their veins and parts of leaves show a recurring pattern throughout.


9 Amazing Fractals Found in Nature