Credit: paulbourke.net
Credit: matplotlib.org
Credit: scipython.com
At some point in your life, you have either heard of the butterfly effect or learned about it. If not, today is your lucky day! The butterfly effect is a scientific explanation to Chaos Theory.
Below are two videos explaining the Butterfly Effect's applications to Chaos Theory (along with further exploration of Chaos Thoery).
https://www.youtube.com/watch?v=1w40fxsyraE
As chaos theory was discovered by the meteorologist Edward Lorenz1, it is only right to discuss how chaos theory applies to Weather Predictions. The smallest initial conditions lead to drastic changes in the outcome. This idea is known as the Butterfly Effect.2 A common example of the butterfly effect is that the flap of a butterflies wings somewhere in Tokyo could impact the weather in Chicago.3
The butterfly effect has been debated between scientists; however, it remains true that seemingly small changes can cause drastic outcomes.4 As Lorenz was using a computer that did large calculations, predicting future weather forecasts is still trying to be improved upon. With the increase in technology, specifically machine learning, predicting the weather has become more accurate. Chaos Theory and the butterfly effect assisted with the understanding of predicting weather in the future. Understanding that small changes in one variable can greatly affect the weather.5 However, predicting the weather far into the future is still difficult, as an abundance of variables must be taken into consideration.
Yet, in some cases, the weather is predictable. As the earth orbits around the sun, we can predict which months will be warmer or colder depending on our hemisphere. Regions around the world have various seasons. The seasons are predictable. However, it is difficult for the weatherman to predict the precise moment Cache Valley will get snow. There are patterns in weather, but predicting the weather is a difficult thing. Thus, Chaos Theory ties closely with weather.
Lorenz attempted to better show Chaos Theory using one single atmospheric condition called a rolling fluid convection. A convection roll is an uncoordianted movement of fluid particles which allows energy transfer between uppoer and lower plates. The model is small, as it can be contained in a 3 dimensional space, and there are few initial variables. Lorenz put in three equations,
\[\frac{dx}{dt} = \sigma(y-x)\] \[\frac{dy}{dt} = \rho x - y - xz\] \[\frac{dz}{dt} = xy - \beta z\]where \(\sigma\) is the ratio of fluid viscosity to thermal conductivity, \(\rho\) is the change in temperature between the top and bottom of the system, and \(\beta\) is the ratio between the width and height of the box. \(x\) represents the convection flow; \(y\) represents the horizontal temperature; and \(z\) represents the vertical distribution.
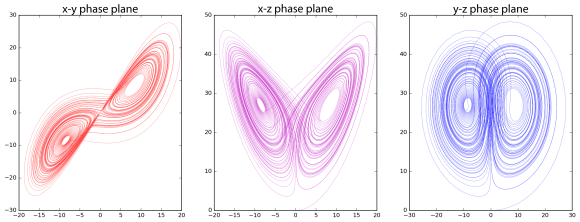
The Lorenz attractor viewed from different planes.
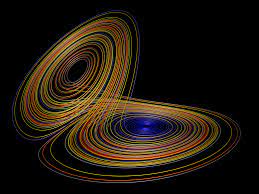
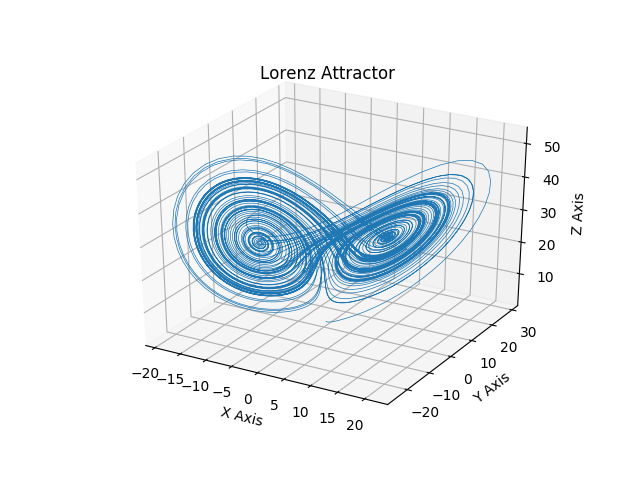
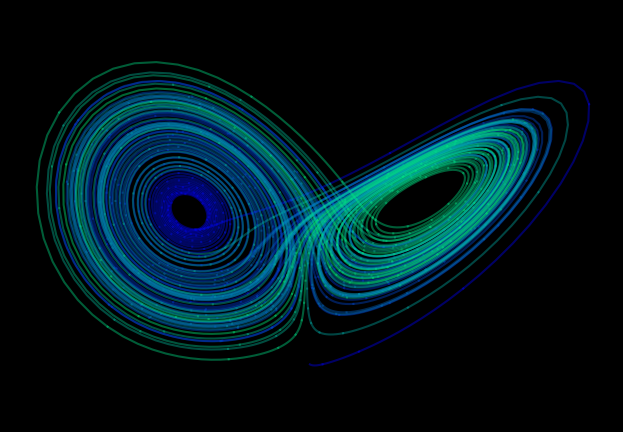
As Lorenz input these values into his computer, the three variables output each represented a dimension in a three-dimensional space. The result in the space was a three-dimensional space known as the Lorenz attractor which is a visual model of Chaos. There is randomness, unpredictability, yet, there is still a pattern.
Various Views of the Lorenz Attractor.
Defnitions provided by Oxford Languages, Merriam Webster, and Google.
.png)
