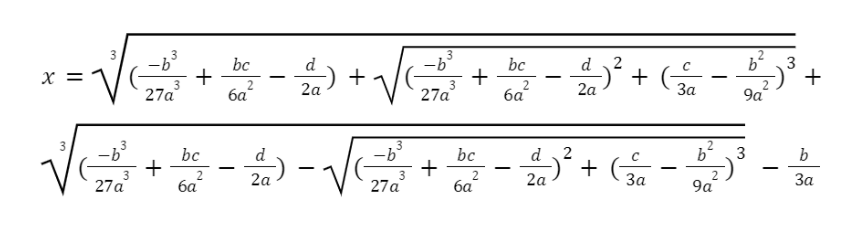A Brief History of Polynomials
Polynomials in their most simple form have been around for several millennia. Quadratic equations (a type of polynomial) were very well known from an early time in history. In fact, most ancient cultures knew how to solve quadratic equations (Wildberger, 2011). The earliest detailed account of the algebra of polynomials comes from around the year 1000 from a mathematician named Abû Bakr al-Karaĵi of Iraq (Burton, 2006). Since then, there have been many advances in mathematics that allow people to better learn, manipulate, write, and graph polynomial functions. These include the Hindu-Arabic number system and the cartesian plane. There were also new symbols being used which allowed people to write things more concretely and concisely (Wildberger, 2011). See the following table:
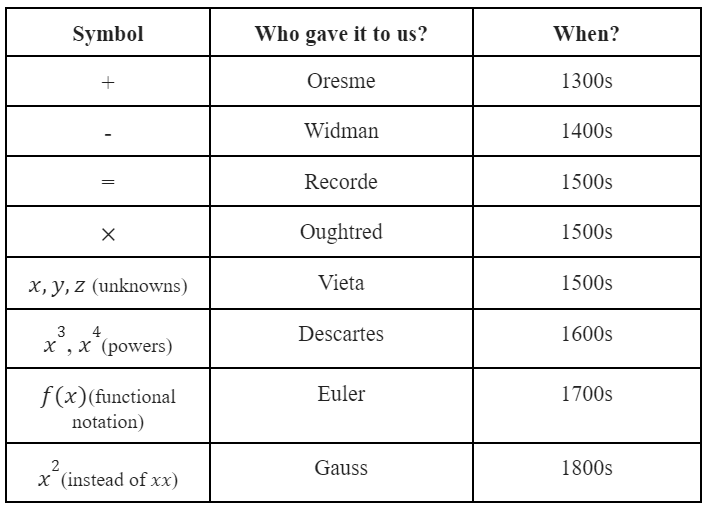
Before the introduction of these symbols, people had to write out math equation in full words and with multiple x’s in a row. It made for some messy computation. Imagine how tedious it would be to keep everything neat while writing out long expressions like polynomials. For examples, the equation \(3x^3+2x^2-4x+3=13\) written out in words is: “three multiplied by some number \(xxx\) plus two multiplied by \(xx\) minus four multiplied by \(x\) plus three is equivalent to thirteen.”
In addition to these useful symbols, there was also an introduction of new ideas about polynomials. Al-Khwarizmi (of Iraq) within the years 815-850 first introduced people to what is now known as completing the square. Rene Descartes (of France) published a book in 1637 which shared some new ideas of polynomials that are still used today. Although he was not the first, he suggested moving all the terms of a polynomial equation to one side and equating it zero (Burton, 2006). This method does have some advantages and is how we generally solve polynomial equations today.
Descartes also indicated that a polynomial equation, \(f(x)\), was divisible by \((x-a)\) if and only if a was a root of \(f(x)\). He wrote a proof of the Fundamental Theorem of Algebra. This theorem says that any polynomial equation of degree \(n\) has \(n\) roots (Burton, 2006).
Descartes also gave us the first glimpse of the quadratic formula in his book as we know it today. What many don’t know is that there exist similar formulas for polynomial equations of degree 3 (seen below) and 4 (due to the length of this formula it is not featured here, but you can see it here: Quartic Formula . This discovery was first published by Cardano of Italy in 1545. While this discovery is no doubt interesting, these formulas aren’t well known. They are much too long to be very practical. There does not exist a formula to solve for the roots of a polynomial equation of degree 5 and higher. This was a discovery made by Niels Henrik Abel of Norway in 1826(Wildberger, 2011). One can only wonder what new discoveries and new methods have yet to be made.