The Basics: What is a polynomial?
The word "polynomial" is composed of two parts. The first is "poly" which comes from the Greek word for "many" and the second comes from the Latin word "nomen" which means "name." In essence the word polynomial means "many names or terms" (Weisstein, 2002). This provides an insight to the nature of polynomials. Polynomials (of one variable) have the following form: \(a_n x^n +...+a_2 x^2 +a_1 x+a_0\)
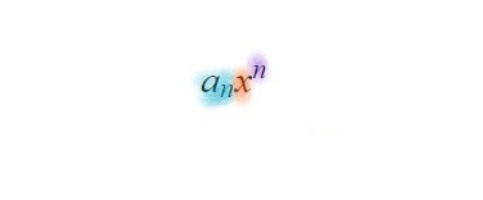
This may look confusing and for some may be overwhelming, so examine the different parts of the first term (seen on the right) The \(a_n\) (blue) is called the coefficient. The small subscript \(n\) on the \(a\) indicates that it is the coefficient that is attached to the \(x^n th\) term. \(x\) (orange) is the variable and \(n\) (purple) in \(x^n\) is the power. A leading coefficient is the coefficient of the term with the highest power. These are important to be able to identify. Try to identify the highest power and the leading coefficient of each of the following polynomial expressions:
\(4x^2-3x+1\)
\(192x^7+65x^3-12x^2\)
\(3x-2\)
\(x\)
\(4x-15x^3+7\)
Classification of Polynomials
While there are many types of polynomials, they are classified and organized in a specific way: by their degree or order. The degree/order of a polynomial is determined by the highest power (Weisstein, 2002). For example, the polynomial expression \(192x^7+65x^3-12x^2\) is of degree 7 and the polynomial expression \(3x-2\) is of degree 1. Polynomials of degree 1 are said to be linear. Polynomials of degree 2 are also called quadratics. These are the most well known kinds of polynomials (Wildberger, 2011)
Solving Polynomial Equations
There are a few different ways to solve polynomial equations. It is important to note however that not every polynomial equation can be solved the same. In general, polynomials of higher degree are more difficult to solve. To begin solving a polynomial equation, one must set the polynomial equal to zero. This is because solving a polynomial equation results in the zeros or roots of that polynomial.
Polynomial Equations of Degree 1
Polynomials of degree one can be solved by isolating the variable. This can be done through algebraic manipulation of the original equation. This may be familiar but below there are examples of polynomial equations of degree 1 and how to solve them to follow. Some tips for solving this type of equation: have a solid knowledge of inverse operations, be sure that whatever is done to one side is also done to the other, and be cautious of the order in which things are “eliminated” first in the equation.
Examples:
- $$5+x=12$$
- $$2y-4=24$$
- $$\frac{3w}{4}+5=15$$
Step 1: Subtract 5 from both sides. This will isolate the \(x\) variable. That leaves \(x=7\).
Step 1: Add 4 to both sides. This leaves \(2y=28\)
Step 2: Divide by 2 on both sides. This isolates the variable and leaves \(y=14\).
Step 1: Subtract 5 from both sides. This leaves \(\frac{3w}{4}=10\).
Step 2: Multiply both sides by 4. This leaves \(3w=40\).
Step 3: Divide both sides by 3. This results in \(w=\frac{40}{3}\).
For a more detailed explanation watch the following video: How to Solve Linear Equations
Polynomial Equations of Degree 2
There are three main methods for solving a quadratic equation. These methods include: factoring, completing the square, and using the quadratic equation. Below are brief summaries of what these methods include and links to applets or videos that will go through these methods more in depth.
Factoring
Polynomial equations of degree two are made of factors; they have two zeros/ roots (by the Fundamental Theorem of Algebra), so there are 2 factors for each quadratic equation (Burton, 2006). By factoring, the polynomial is, in essence, broken down into these factors (Weisstein, 2002). This can be done by finding two numbers whose sum is \(b\) and whose product is \(ac\) for a polynomial equation of the form: \(ax^2+bx+c=0\) (Brown, 2020). The best way to understand how this works is to go through an example. Take the polynomial equation: \(x^2+2x=15\).
Step one: Make sure the polynomial equation is in the right form: \(ax^2+bx+c=0\). The example polynomial equation is not in the correct form but subtracting 15 from both sides fixes the problem: \(x^2+2x-15=0\).
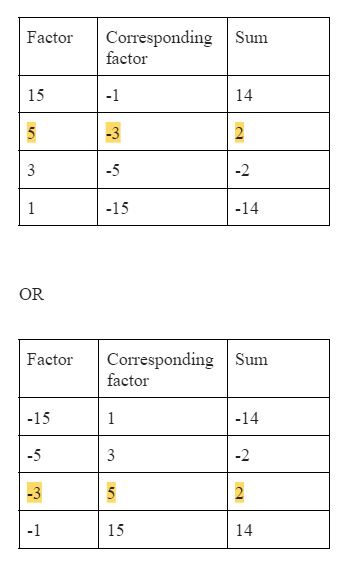
Step two: Next find two numbers whose sum is equal to \(b\) and whose product is \(ac\). For the example, \(b=2\) and \(ac=-15\) (\(a\) is just 1). Listing the factors of \(ac\) can be helpful. In this case the factors of ac are -15, -5, -3, -1, 1, 3, 5, 15. Putting these factors in a table will help better visualize their sum/difference. Here one may notice that 5 and -3 add to give 2 and multiply to give -15.
Step three: Break down the polynomial. For quadratic equations, the factors will have the form:\((x-h)(x-g)=0\). Here h and g are replaced by the factors of ac that we found. In this example, those are 5 and -3. So the factored polynomial is : \((x-5)(x+3)=0\). Notice that the sign changes because \(x--3=x+3\). To ensure that the polynomial is correctly factored one may FOIL/expand the factored equation. It should match the original polynomial.
Step four: Now that the polynomial is factored it is very easy to find the \(x\) values that when plugged into the polynomial equation would result in 0. If either term (meaning \(x-h\) or \(x-g\)) is zero then the whole thing is zero. This is because any number multiplied by zero is zero. So set each individual factor to zero. Since our polynomial is set to zero, we want numbers that when plugged in will result in zero. For example, \(x-5=0\) and \(x+3=0\). So \(x=5\) and \(x=-3\) (Weisstein, 2002). These are the solutions to this polynomial equation. These are referred to as zeros. People call these zeros because when these values of x are plugged in, the equation will equal zero. It is also where the graph of the corresponding polynomial function intercepts the \(x\) axis.
This method will not work for every quadratic equation. Every polynomial of degree two is made up of two factors, but not every polynomial equation has integer zeros or roots.
For additional instruction watch the following video: How to Solve Quadratic Equations by Factoring
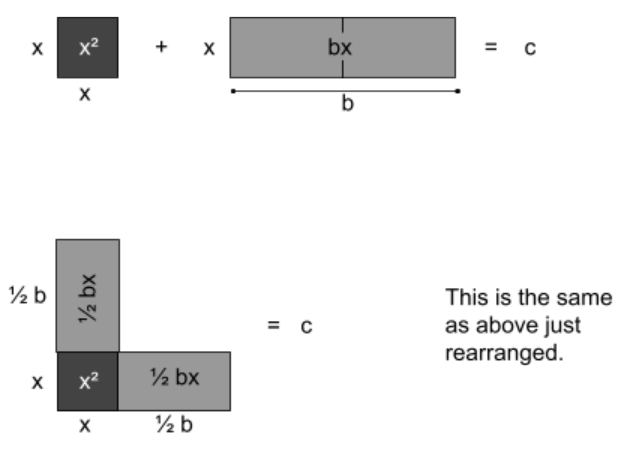
Completing the Square
This method gets its name from the geometrical connection it has. When one uses this method they are quite literally completing the square (Hughes). Visit the following link for more detail on this: Completing the Square Geometrically and look at the images included with each step to better understand this. The steps for completing the square are as follows:
Step one: Put the polynomial equation in the form: \(ax^2+bx=c\) with \(a=1\) (if necessary). This can be seen geometrically (notice that side lengths and areas are labeled) below:
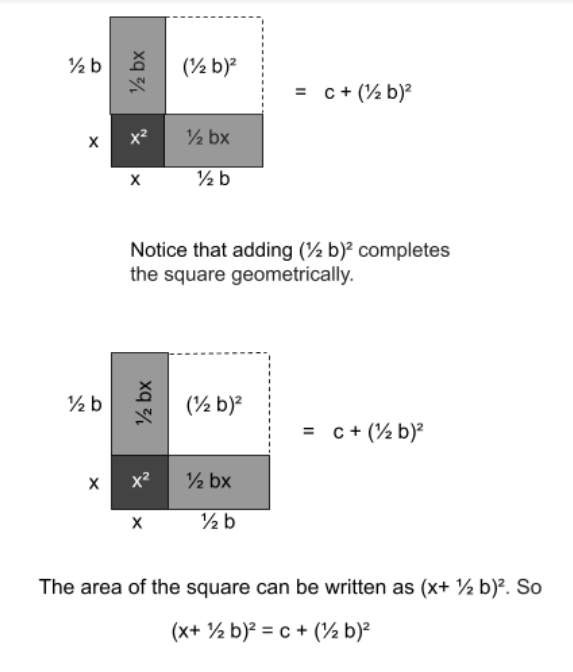
Step two: Add \((\frac{1}{2}b)^2\) to both sides of the equation.
Step three: The left side of the equation simplifies to \((x+\frac{1}{2}b)^2\)
Step four: Solve for \(x\) (Phillips).
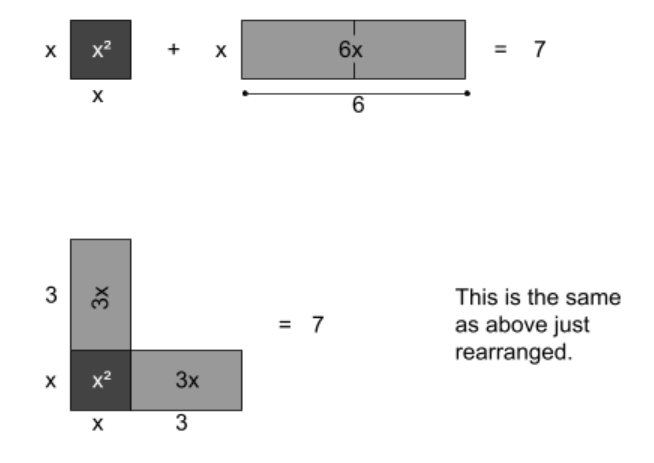
Below is an example of completing the square for the polynomial equation \(x^2+6x-7=0\).
Step one: We put our polynomial equation into the form \(ax^2+bx=c\) adding 7 to both sides of the equation. This results in: \(x^2+6x=7\)
Step two: \(b=6\) , so plug that into \((\frac{1}{2}b)^2\). That gives us \((\frac{1}{2}6)^2=3^2=9\). So add 9 to both sides of the equation: \(x^2+6x+9=7+9\)
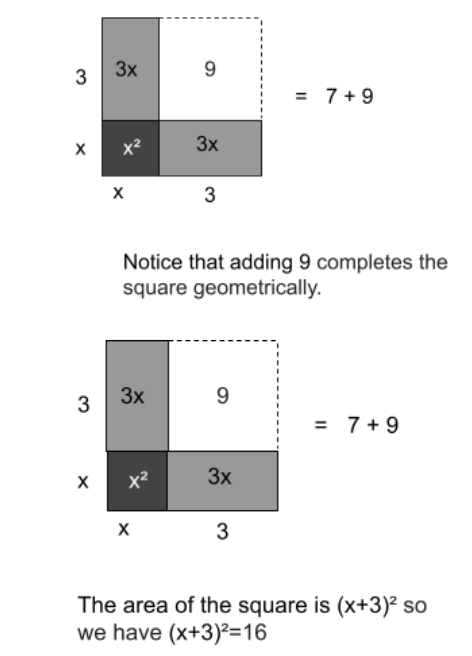
Step three: The left side of the equation can simplify to \((x+12b)2\). Recall that \(b=6\), so we have \((x+\frac{1}{2}6)^2\). So our equation becomes \((x+3)^2=16\)
Step four: Now we solve for the \(x\) variable. \((x+3)^2=16\rightarrow\sqrt{(x+3)^2}=\pm16\rightarrow(x+3)=\pm4\)
At this part of step four we have \(\pm\sqrt{16}\) . This is because \(\sqrt{16}\) results in two answers; both 4 and -4 squared are 16: \(4\times4=16\), \(-4-4=16\). This is vital. Keep this in mind because quadratic equations each have two roots (Link to Fundamental Theorem of Algebra in History section). Continuing with the example, there are two equations to solve: \(x+3=4\) and \(x+3=-4\). This results in \(x=1\) and \(x=-7\).
For a more thorough explanation watch the following video: Completing the Square
Quadratic Formula
This method will work for any quadratic equation. A polynomial equation of degree two with general coefficients is \(ax^2+bx+c=0\). The quadratic formula is derived from completing the square with general coefficients (Weisstein, 2002). This process can be seen below:
Step one: We have \(ax^2+bx+c=0\). Make the leading coefficient 1. So divide by \(a\). This leaves: \(x^2+\frac{b}{a}x+\frac{c}{a}=0\). We also want our equation to be of the form: \(ax^2+bx=c\) . So we subtract \(ca\) from both sides. We are left with \(x^2+\frac{b}{a}x=-\frac{c}{a}\).
Step two: Add \(\frac({1}{2}b)^2\)to both sides of the equation. In our case \(b=ba\) , so \((12b)2=(b2a)2\). That leaves \(x^2+\frac{b}{a}x+(\frac{b}{2a})^2=(\frac{b}{2a})^2-\frac{c}{a}\).
Step three: The left side of the equation simplifies to \((x+\frac{1}{2}b)^2\). Recall that in our case \(b=ba\) This leaves \((x+\frac{b}{2a})^2=(\frac{b}{2a})^2-\frac{c}{a}\).
Step four: Solve for \(x\). This means that we need to isolate the \(x\) variable. We have \((x+\frac{b}{2a})^2=(\frac{b}{2a})^2-\frac{c}{a}\).
First we take the square root of both sides to get rid of the power of 2. This results in \(\sqrt{(x+\frac{b}{2a})^2}=\pm\sqrt{(\frac{b}{2a})^2-\frac{c}{a}}\). Remember here that when taking the square root of something that this results in two answers, thus we add in the (regardless of the sign squaring any number will always result in a positive number).
This leaves: \(x+\frac{b}{2a}=\sqrt{(\frac{b}{2a})^2-\frac{c}{a}}\).
Then we subtract \(\frac{b}{2a}\) from both sides: \(x=-\frac{b}{2a}\pm\sqrt{(\frac{b}{2a})^2-\frac{c}{a}}\).
\(x\) has now been isolated, so simplify the right side. Expand \((\frac{b}{2a})^2\). That leaves: \(x=-\frac{b}{2a}\pm\sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}\).
Now, combine the fractions in the square root. For this one needs a common denominator. So multiply the top and bottom of \(-\frac{c}{a}\) by \(4a\). This leaves: \(x=-\frac{b}{2a}\pm\sqrt{\frac{b^2}{4a^2}-\frac{4ac}{4a^2}}\).
Now these fractions can be combined. This leaves: \(x=-\frac{b}{2a}\pm\sqrt{\frac{b^2-4ac}{4a^2}}\).
Recall that this is equivalent to \(x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac}}{\sqrt{4a^2}}\). The denominator can be simplified to \(2a\). This leaves: \(x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}\).
This can be rewritten as \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\). This is the quadratic formula. This formula is used for quadratic equations. To use this formula one must ensure that the polynomial is in the form \(ax^2+bx+c=0\). Then, the values for \(a, b,\) and \(c\) are inputted and computations made. This results in the two roots of the polynomial equation (thus the \(\pm\)in the formula). An example is displayed below:
For the polynomial equation \(3x^2+5x+1=0\) so \(a=3, b=5,\) and \(c=1\). Input these values into the formula. That results in \(x=\frac{-5\pm\sqrt{(5)^2-4(3)(1)}}{2(3)}\). With some simplification this becomes: \(x=\frac{-5\pm\sqrt{25-12}}{6}\). With more simplification and what is left is : \(x=-\frac{5\pm\sqrt{13}}{6}\). So \(x=-\frac{5+\sqrt{13}}{6}\) and \(x=-\frac{5-\sqrt{13}}{6}\). These may appear odd, but that is the final result. In order to check this answer one could plug it back into the original equation and see if the result is truly zero.
For further explanation watch the following video: Solving Quadratic Equations Using the Quadratic Formula
Polynomial Equations of Degree 3 and Above
It can be more difficult to solve polynomial equations of degree 3 and above. For polynomials of degree 3 and 4, there exists formulas ( Cubic Formula and Quartic Formula ). These, however, are not easy to use and there are no formulas for solving polynomial equations of degrees 5 and higher (Wildberger, 2011). The stratagem for solving these polynomials is in breaking them down into polynomials of smaller degree by pulling out common factors. These parts become more manageable and other methods mentioned earlier can be used to solve them (Brown, 2020). With bigger polynomials, this is best done by grouping the terms and pulling out common factors. This does not work for every polynomial. An example of this process is shown below.
Take the polynomial function \(f(x)=x^3-4x^2-3x+12\). Group the first two terms together and the last two terms together: \(f(x)=(x^3-4x^2)-(3x-12)\). Then pull out common factors. The first group has an \(x2\) in common and the second group has a 3 in common. Pulling these out leaves: \(f(x)=x^2(x-4)-3(x-4)\). Notice that we have \((x-4)\) in each group now. Simplifying this leaves: \(f(x)=(x-4)^2(x^2-3)\). Now there is a factor and a degree two polynomial. Set the factor equal to zero: \((x-4)^2=0\). Taking the square root of both sides results in \(x-4=0\). Adding 4 to both sides then results in \(x=4\). Next, we solve for \(x\) for the degree 2 polynomial so set : \(x^2-3=0\). Add three to both sides: \(x^2=3\). Take the square root of both sides and the result is: \(x=3\). These are the other two solutions (so we have found all three solutions). Alternatively, the quadratic formula can be used to find the roots of the quadratic (UCSB, 2016). \(x^2-3=0\) is in the form \(ax^2+bx+c=0\) so we can plug in our values. \(a=1\), \(b=0\), \(c=-3\). So we have \(x=\frac{-(0)\pm\sqrt{(0)^2-4(-3)(1)}} {2(1)}= \frac{\pm\sqrt{12}}{2}=\frac{\pm2\sqrt{3}}{2}=\pm\sqrt{3}\).
For additional help factoring cubic polynomials watch the following video: Factoring Cubic Polynomials
Another method for solving polynomials of higher degree includes the use of synthetic division and the Rational Roots Theorem. Watch the video below for an explanation of how to use this method.
For extra help with this method also watch the following video: Rational Root Theorem
Overall, one of the best methods for solving polynomials of higher degree is graphing them. The following is an online graphing calculator that is easy to use: Graphing Calculator .
Graphs of Polynomial Functions
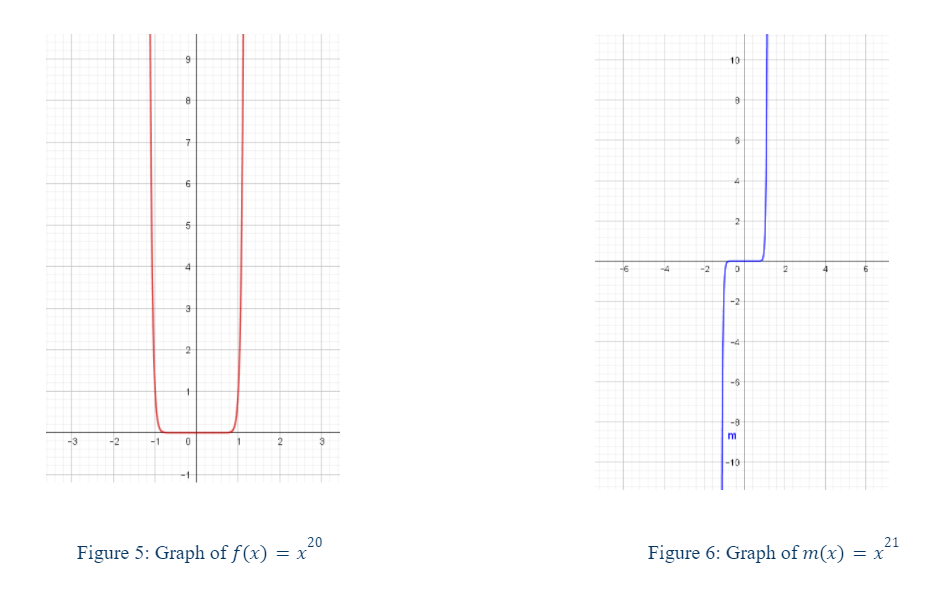
The focus here is on the graphs of polynomials with degrees greater than 1. This is because a polynomial of degree 1 is simply a line. Below in figures 1, 2, 3, 4, 5, and 6 we see the graphs of 6 different polynomial power functions. Notice any patterns? One may note that polynomial functions with an even degree are symmetrical about the y-axis. With functions of even degrees the tails both go in the same direction. With functions of odd degree the tails go in opposite directions (Abramson). This holds true for power functions with negative leading coefficients too; the only difference is that these graphs are flipped upside down. As the degree increases the function seems to “flatten” around the origin (at least in the cases of the parent functions; in transformed functions the flattening will occur around the vertex or point of inflection for odd degrees). Notice also that the functions become more narrow and steep.
These observations are important because one can use this knowledge of the end behavior of different power functions to later sketch other functions. The end behavior describes the behavior of a function as \(x\) approaches positive and/or negative infinity (Abramson).
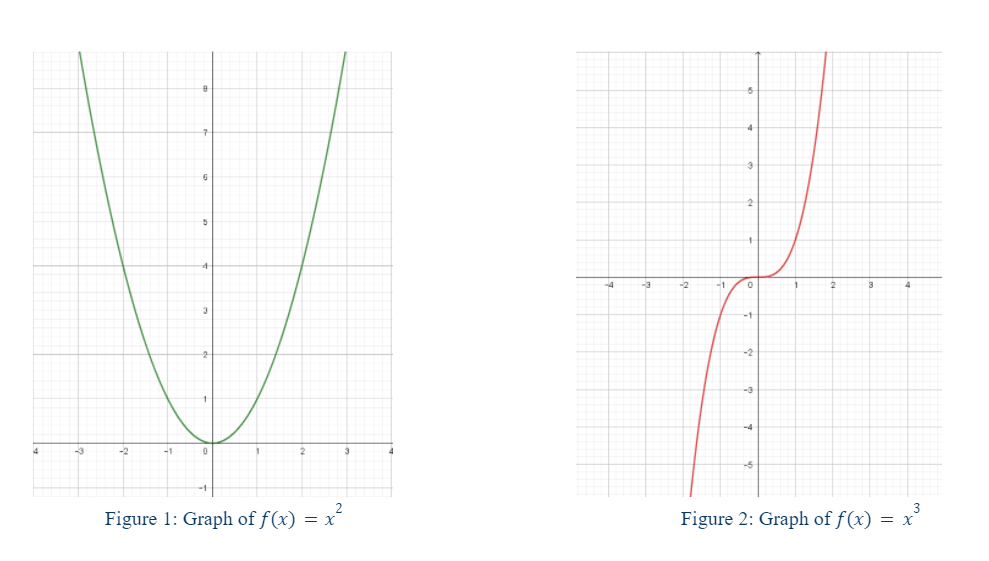
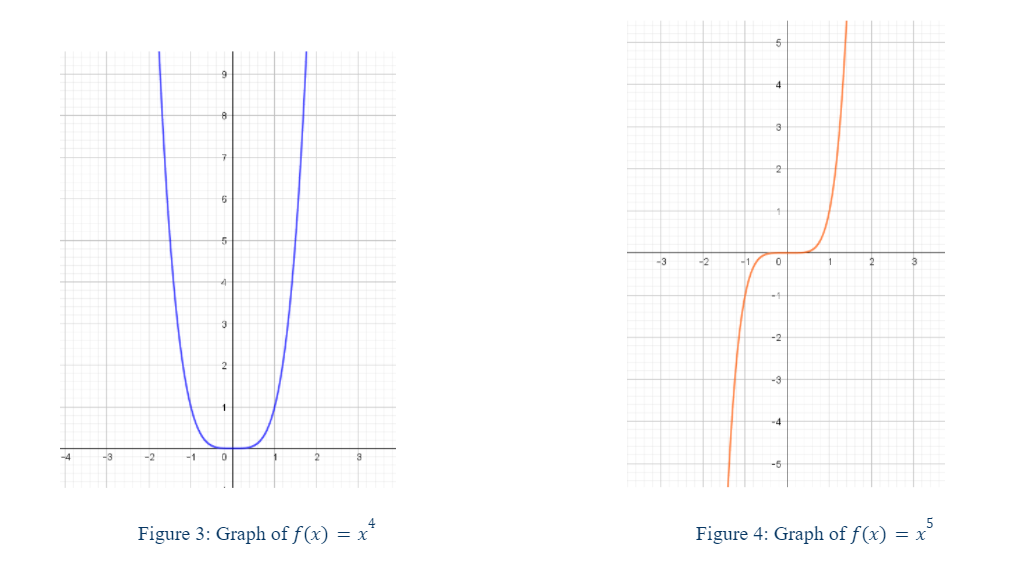
Sketching Graphs of Polynomial Functions
There are 4 steps to sketching graphs of our polynomial functions:
- Factor the polynomial (if necessary and possible).
- Find the x and y intercepts (as ordered pairs).
- Determine the end behavior.
- Put it all together and graph.
The following is an example that goes through each step of this process. The polynomial used is \(f(x)=(x-1)(x-2)(x+2)^2\).
Step 1: In this case the function is already in factored form. If this is not the case, break down the polynomial into its factors if possible.
Step 2: Find the \(x\) and \(y\) intercepts. The \(x\) intercepts are easy to find because the function is factored. As previously mentioned \(x\) intercepts are also known as roots, solutions, or zeros of a polynomial equation/function. This is because it is at those values of \(x\) where the function crosses the\(x\) axis because that is where the equation equals zero. These written as ordered pairs are: \((1,0)\), \((2,0)\), \((-2,0)\). To find the \(y\) intercept input in zero for \(x\) like so: \(f(0)=(0-1)(0-2)(0+2)^2\). This simplifies to become: \(f(0)=8\).This means that the \(y\) intercept is at \((0,8)\).
Step 3: Next, determine the end behavior. This is best done through finding the degree of the polynomial and creating a sign chart. The polynomial in our example
is of degree 4. This was calculated by adding the powers of each factor. Based on this our function will have tails going the same direction.
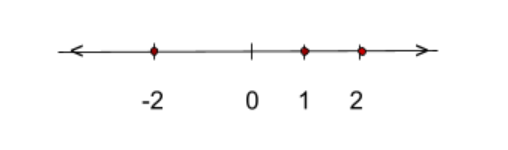
In other words, if one tail is going up, the other will too and vice versa with downward tails. To create a sign chart, make a line (this will represent the \(x\) axis)
and place the \(x\) intercepts on it. To the right is a the beginning of a sign chart for the example polynomial.
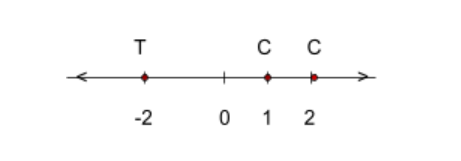
Next, one must find the multiplicity of each factor. The multiplicity is the number of times a zero of a polynomial shows up in the set of zeros (Weisstein, 2002).
In the example, \(1,0)\) has a multiplicity of 1, \((2,0)\) has a multiplicity of 1, and (-2,0) has a multiplicity of 2. \(x\)intercepts with odd multiplicities cross the \(x\) axis and
intercepts with even multiplicities touch the \(x\) intercepts (Abramson). Why this is the case can be explored by using this Multiplicity Applet. This information can be
added to the sign chart with “C” to mark at which intercepts the function crosses the \(x\) axis and “T” to mark where the function touches the \(x\) axis. See the figure to the left.
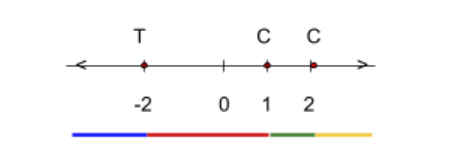
To finish the sign chart, plug in values from in between the \(x\) intercepts to have an idea of what the function’s \(y\) values are: negative or positive. The figure to the right
has colored lines for each section from which we will pull an \(x\) value to plug into our polynomial.
For this particular example, the \(x\) values that will be plugged in are -3, 0, 1.5, and 3. These are fairly arbitrary; they just need to be within each interval.
Shown below are the calculations for each inputted value. It is not important to know what the result is, it is only important to know whether it is positive or negative.
\(f(-3)=(-3-1)(-3-2)(-3+2)^2=(-4)(-5)(-1)^2=20\rightarrow\) Positive result
\(f(0)=(0-1)(0-2)(0+2)^2=(-1)(-2)(2)^2=2(4)=8 \rightarrow\) Positive result
\(f(1.5)=(1.5-1)(1.5-2)(1.5+2)^2=(.5)(-.5)(3.5)^2=(-.25)(12.5)=-3.0625\rightarrow\) Negative result
\(f(3)=(3-1)(3-2)(3+2)^2=(2)(1)(5)^2=50\rightarrow\) Positive result
Add these details to the sign chart and the sign chart is complete (see below).
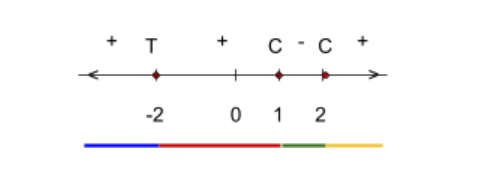
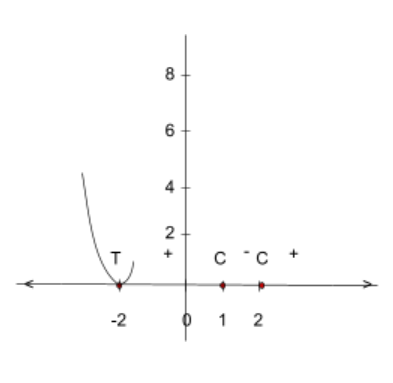
Step 4: Finally, one may begin to sketch the graph. Use the sign chart as a base. Below are sketches that show the process that one might go through to sketch this polynomial (from left to right). To the left of -2 on the \(x\) axis it is known, by the sign chart, that the function has positive \(y\) values. This part of the function is above the \(x\) axis. The “T” above the -2 on the \(x\) axis means that the function will touch (but not cross) the \(x\) axis at that \(x\) value. From there the sign chart shows that the function continues to have positive \(y\) values (thus the sketch shows the function touching the \(x\) axis and bouncing back to the positive values)(Abramson).
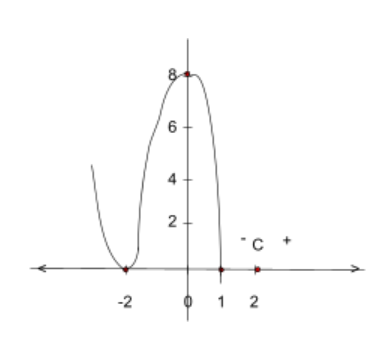
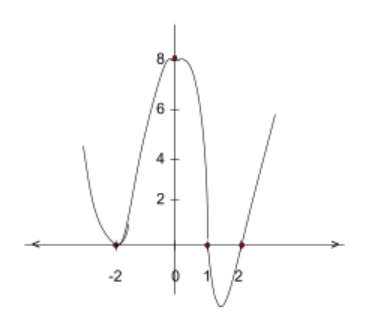
The figures below continue to sketch the polynomial function using the information collected: the\(y\) intercepts, where the function is negative, where the function is positive, and where the function crosses the \(x\) axis. The figure on the right is the final sketch of \(f(x)=(x-1)(x-2)(x+2)^2\).
For additional help sketching polynomials see the following link: Sketching Polynomials .