Polynomials in Real Life
Polynomials are used in everyday life. Try to calculate how much it would cost to buy 5 candy bars. In order to calculate how much it would cost to buy five we would take \(5x=y\) for \(x\) being the cost of the candy bar and \(y\) being the total cost of all five candy bars. Notice that the equation we used is a polynomial equation and works for any candy bar. This use of polynomial equations is very common.
Polynomial functions are also used to make predictions. In the field of statistics, people fit linear functions to data collected in order to make predictions or better explain the relationships between variables. This means that based on data, a linear equation was found that allows one to predict one variable based on the other. The following link contains an article that explains this further and uses the example of height and weight: Simple Linear Equations .
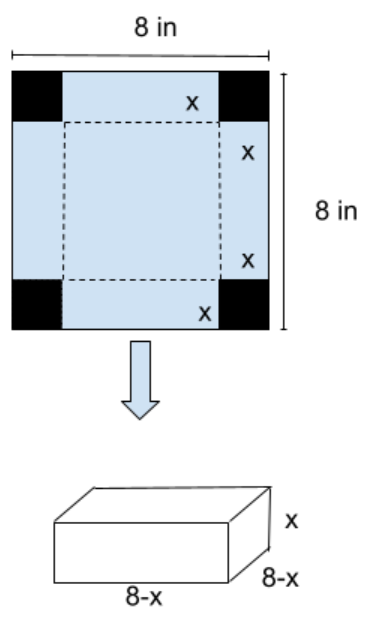
Polynomial functions can help find maximum values for things like revenue or volume. For example, given a piece of paper with a length and width of 8 inches with squares cut out on each corner and folded along the dashed lines, and glued or taped together along the \(x\) edges (see figure to the right for reference), what has been created? The answer is a box (without a top). The real task is to make a box with the largest volume possible. In other words: what measurement of \(x\) gives us the biggest box? This problem can be solved using a polynomial equation. The first step would be to write the volume of the box in terms of \(x\). The volume of a rectangular prism (aka the box) is length*height*width. This means that the volume of the box is: \(V=(x)(8-x)(8-x)\). This expanded is: \(V=x^3-16x^2+64x\). A graph of this will reveal what the x value needs to be for maximum volume. Try it! Use this Graphing Calculator . Make sure to take into account the possible value of x based on the context of the problem (\(x\) can only take on values between 0 and 4, why?) (Strader, 2017).
What value of \(x\) fives the greatest volume? What is that volume?: After examining the graph the highest point between 0 and 4 was the point \((2.667, 75.852)\). This means that for maximum volume \(x\) has to be 2.667 inches and will have a volume of \(75.852 in³\).
For a similar more in depth example see the following link: Applications of Polynomial Functions