Hyperbolic and elliptic geometries serve as the gateways to infinitely diverse forms of non-Euclidean geometry. There are many mathematical tools to faithfully capture, relate, and define how these spaces behave and what it would be like to inhabit them. Such tools fall under the purview of differential geometry which helps us to quantify the local differences between a non-Euclidean space and Euclidean space at every point [8]. We want to quantify how much and in what way the fifth postulate is broken at every point in our space. 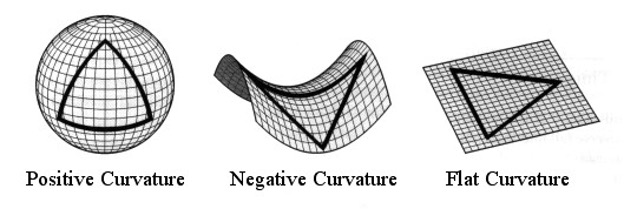We want to measure the intrinsic curvature of a surface. In two dimensional spaces we only need a single real number to capture the intrinsic curvature at around point. One way of doing this is by building a small circle of constant radius, like the ancient Egyptians, and then measuring its area. If we do this on the surface of a sphere, we find that the area of our circle will be less than a circle of the same radius in flat space. Whenever we have a point around which this occurs, we say there is positive curvature at that point. When this happens, we will also find that straight lines that start off parallel tend to converge around that point, and that the internal angles of triangles around that point have angles that sum to more than 180 degrees [9].

On a hyperbolic plane, or a saddle, we find that circles have more area than those constructed from the same radius in flat space. This implies that the space has negative curvature. Straight lines that begin parallel will diverge, and triangles have angles that sum to less than 180 degrees [9].

Euclidean space is called “flat” as it has zero curvature everywhere, and the parallel postulate always holds by definition. Perhaps initially surprising, a cylinder has no intrinsic curvature under this or any other definition. We can make sense of this in considering how easy it is flattened out a cylinder without it tearing or buckling, compared to the impossibility of such a task with a sphere (tearing) or saddle (buckling).

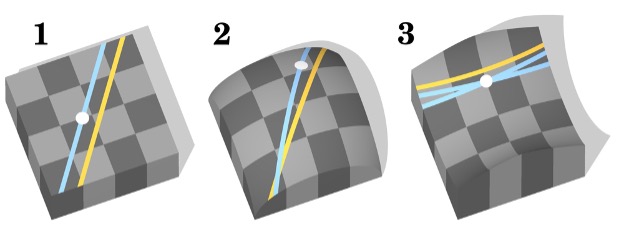
We can better understand why lines coverge in spaces with positive curvature, like spheres, by imagining the following: consider two people leaving from the equator towards the North pole. While their paths initially appear parallel, they inevitably converge at the North pole. This is not because they were pulled together through space, but because the space between them shrunk! Again, the opposite is true for regions of negative curvature where lines that begin parallel always diverge as the space between them grows [9].

The surfaces discussed thus far have been continuous in nature, but curvature also shows up in polyhedra, three-dimensional shapes with flat polygonal faces. A lot of the tools for understanding discrete curvature are useful to 3D animators and modelers. This is because 3D models are represented in computers by surfaces of triangles or other polygons glued along common edges called meshes [8]. While you don’t have to think about geometry when watching Shrek, there is a great deal of mathematical wisdom that goes into animation technology and techniques. So, how can we import our understanding of curvature in the continuous context to the discrete one?

Let’s start with a simple shape, the surface of a cube. If we try to find where the parallel postulate fails, we won’t succeed on the faces which are polygonal pieces of flat planes, nor the edges which we can move across without noticing a change. However, we can find curvature around the vertices, or corners, of the cube. We can see this by folding out the cube into its net, shown in the applet below. There is clearly pi/2 radians of paper missing around each corner relative the flat paper! We thus define the curvature as 2pi – theta, where theta is the missing angle. In the case of the cube each corner then has curvature 3/2 pi at each vertex. A flat piece would have 2pi-2pi =0 curvature. We can see this curvature easily from the outside, but how would something living in the surface know it has curvature? It could build a circle and measure its area, it could see how parallel lines move around the vertex, it could see that the angles of a triangle sum to 270 degrees (red dashed line is a triangle in applet). A traditional way to measure curvature is to slide in a loop without rotating in space, but see if you still return to your original location rotated due to the space itself. If we have a surface of negative curvature, we will get an overlap in paper instead of a deficit. For this reason we would need to use multiple pieces of paper since we can’t simply cut a saddle out of paper.