With the knowledge that there is no single and true tree of geometry we are left wondering, “what’s the geometry of our universe? It appears flat, but can we be sure?” The answer to this question starts with Newton’s First Law:
An object in motion stays in motion along a straight line through sapce at constant speed unless acted upon by an outside force. This gives a prescription for finding how the straight lines in our universe behave, which we can use to measure curvature and determine the geometry of the space around us; we just need to understand how things move when they aren’t acted upon by forces. Such investigations became massively significant in the beginning of the 20th century, and it was at this time that we began to understand the necessity of interpreting time as a dimension. We can get a sense of how to visualize this with this video. When we take this step, Newton’s first law can be reinterpreted as An object in motion stays in motion along a straight line through spacetime unless acted upon by an outside force. The constant velocity requirement in the first law is really a demand that objects travel on straight lines through space and time, or spacetime! Motion and physics became matters of geometry. Even when you aren’t moving through space (relative to yourself) you can't help but move through time.

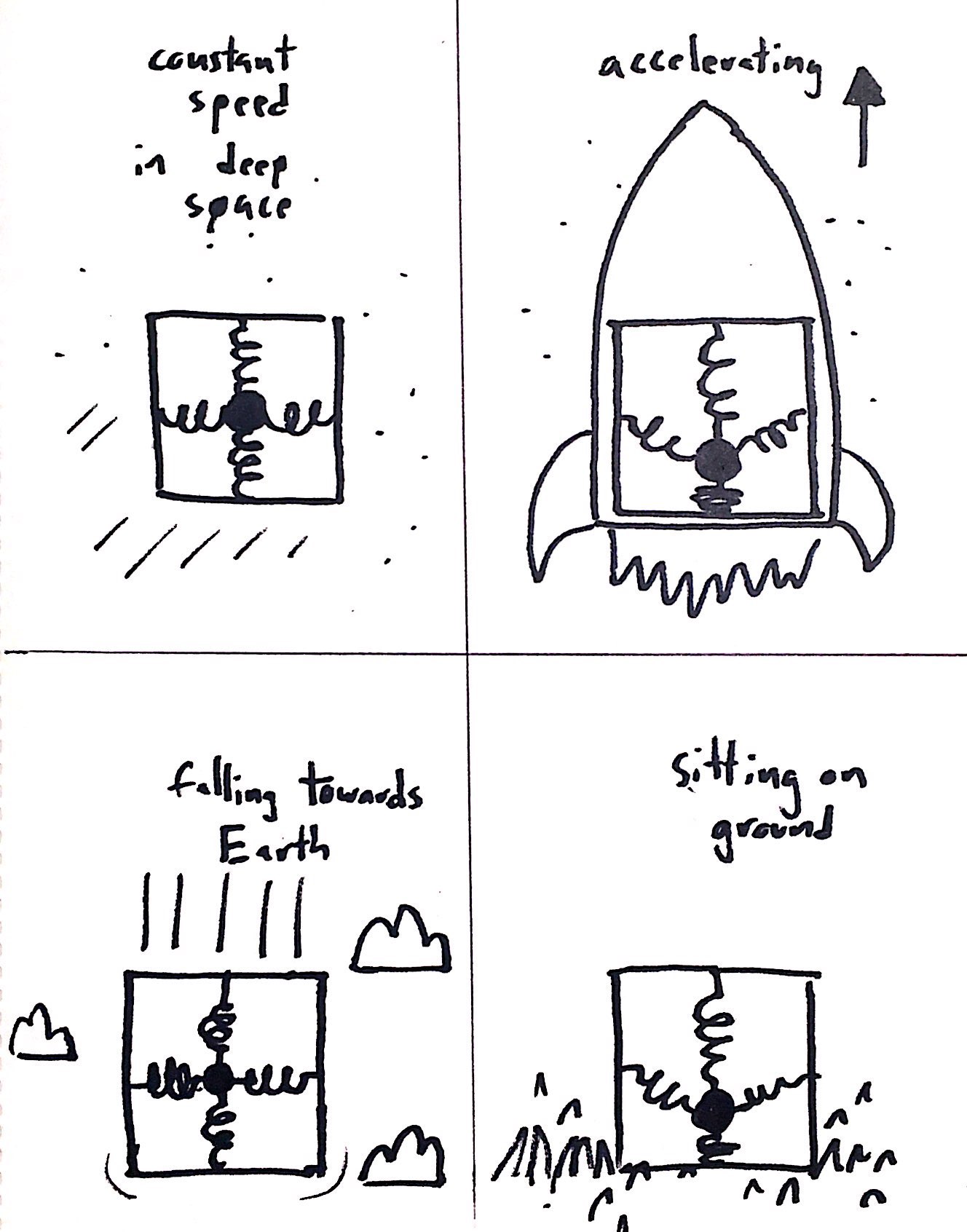Let’s get serious about finding these straight lines. We can construct a box with springs connected to each face suspending a weight in its center. When this device has no forces acting on it, the ball will stay equidistant from the walls of the box. When it is accelerated, or being acted upon by a force, the ball will move to the side opposing the force. This is the same reason you feel pressed into your seat when you push on the gas pedal. So we can find the straight lines through spacetime by simply tracing paths along which the ball stays at the center of the box. If we built this box, we would quickly find something bizarre. Setting the box on the ground, we would find that it would say “I am accelerating upwards!” Can this be? When we drop it, the box says “No forces are acting on me, therefore I am traveling along a straight line” as it falls.

This occurs because the “force” of gravity increases in strength with mass and causes objects of different masses to fall together. We can see this by dropping a feather and a bowling ball in a vacuum to avoid air resistance: they will hit the ground at the exact same time. So, the box, the springs, and the ball in its center all move downwards together. We are forced into accepting that we are actually accelerating while sitting down, and only traveling on straight lines through spacetime as we fall. If the paths of falling objects are straight lines, how can we use that to grasp the geometry of spacetime? We start with our knowledge of how things fall under Newtonian gravity. If two objects are dropped above the Earth at different heights, they will begin to separate as they fall since gravity is stronger for the object closer to Earth. This separation is indicative of negative curvature. If two objects were dropped down a shaft through the Earth, they would tend to converge since Gravity decreases in strength towards the center of the Earth (if you were at the center you would be pulled equally in all direction). These ideas are manifested in the applet below. This applet allows you to click and drag the starting position of object A, and control its initial velocity using a slider. We can see the straight path it would trace through spacetime, and how this would appear to us with time as a dynamic variable. There is also the ability to turn on a second object B to see how the curvature is negative outside of the Earth and positive inside. This is easiest to see by setting both initial velocities to 0 so that they start parallel. We can also see that an object starting parallel with Earth's surface decends inward, implying that the surface is not a straight line and is instead accelerating. Gravity is a manifestation of curvature, and mass causes gravity. This is why we say that massive objects curve spacetime [12]. The shape of the universe depends on its contents.