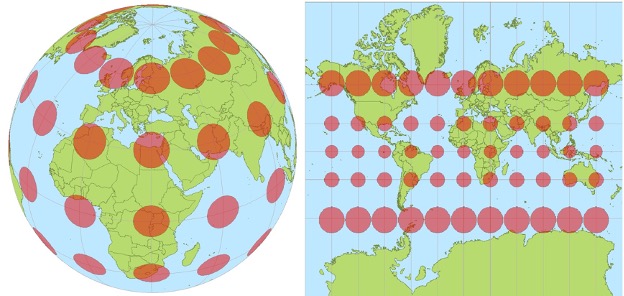
For as long as we have drawn maps to better understand the shape of our Earth, cartographers have reckoned with the impossibility of perfectly representing a round planet on a flat map. As maps stretch to encompass larger portions of the Earth, distortions in the sizes and angles of objects inevitably enter the picture [6]. These distortions become painfully obvious on maps that portray the entire globe. The Mercator projection is a map shown in a variety of classrooms all around the world and owes its popularity to its usefulness in seafaring. It is a projection that maintains angles so that sailors can successfully use compasses in navigation [11]. The price it pays for this feature is extreme distortion of surface areas as one nears the poles, and one can easily compare the distortions here: thetruesizeof.

Each projection comes with tradeoffs, misleading and some ways and helpful in others. While we think of the Earth as sitting inside of three dimensional Euclidean space, geometry restricted to its surface is essentially non-Euclidean. This is because all straight lines that begin parallel on a sphere, like those starting from the equator, inevitably intersect. One reason this non-Euclidean nature was not immediately apparent is because the light from objects is not restricted to the Earth’s surface, so we can look out to the stars and feel the warmth of the sun, and know that there is something beyond the surface.

In a leap of imagination, consider what it would be like if light was confined to or near the surface of the Earth. As you looked toward the horizon you could see on and on as the light bent around the Earth until a mountain obscured your view, and if you stood on the highest mountains with the best telescopes, you could see your own head since the light would circle all the way around the Earth [13]! While light is not confined to the geometry of the Earth’s surface, our modes of transportation like cars and airplanes are. Spherical geometry is a subset of Elliptical geometry where we characterize the fifth postulate by stating that given a straight line every other straight line will eventually intersect it.