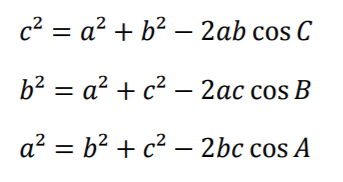Angles
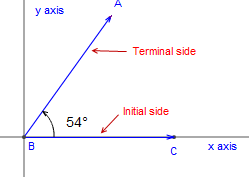
One key concept of trigonometry is angles. Trigonometry focuses on the relationships between sides of a triangle
and the angles formed by the sides. First off, an angle is measured by the amount of rotation between the initial and
terminal sides of the angle (the starting point and ending point). There are several different ways that angles are
measured, although some are more common and used more often than others (Johnson, 2016).
***Angles can be measured in degrees. This is one of the most common ways of measuring angles. In degree measurements,
a circle is 360 degrees- which is due to the Babylonians. As was mentioned in the History Page, the Babylonians used a base
60 as their unit of measurement. The following paragraph from “A History of Pi” by Petr Beckmann explains what the
Babylonians knew about circles and 360, and why we use 360 degrees as the measure of a circle today (Sachs).
“In 1936, a tablet was excavated some 200 miles from Babylon. Here one should make the interjection that the Sumerians were first to make one of man's greatest inventions, namely, writing; through written communication, knowledge could be passed from one person to others, and from one generation to the next and future ones. They impressed their cuneiform (wedge-shaped) script on soft clay tablets with a stylus, and the tablets were then hardened in the sun. The mentioned tablet, whose translation was partially published only in 1950, is devoted to various geometrical figures, and states that the ratio of the perimeter of a regular hexagon to the circumference of the circumscribed circle equals a number which in modern notation is given by 57/60 + 36/(60^2) (the Babylonians used the sexagesimal system, i.e., their base was 60 rather than 10). The Babylonians knew, of course, that the perimeter of a hexagon is exactly equal to six times the radius of the circumscribed circle, in fact that was evidently the reason why they chose to divide the circle into 360 degrees (and we are still burdened with that figure to this day). The tablet, therefore, gives ... π = 25/8 = 3.125 (Sachs).”
The Babylonias were able to relate the circumference of a circle to the number of parts (or angles) that make up a
circle. Modern trigonometry has adopted this way of measuring angles just as the modern world has adopted many other
practices put in place by the (Sachs).
***Another common method of measuring angles is by radians. In radian measure, the angle of an entire circle is 2 π. The following paragraph written by John Papiewski explains the relationship between angle measurements in radians and the length of the radius of the circle. “The radian comes from the length of the circle’s radius. The segment of a circle’s circumference that corresponds to the angle made by two radius lines makes an arc. The angle that this arc creates, when you draw lines from its starting and end points to the circle’s center, is one radian. Though the radian might appear odd and complicated at first, it simplifies equations in math and physics (Papiewski).”
***A third way of measuring angles is measuring by revolutions. This is a less common way of measuring angles, but still
useful in some situations. An angle measure by revolution is the measure of the angle formed when the initial side rotates
all the way around its vertex until it reaches its starting position. Measuring an angle by revolutions simply counts the
number of times the initial side rotates all the way around the circle until it is back in its starting position (Measuring Angles, 2019).
Trigonometric Ratios
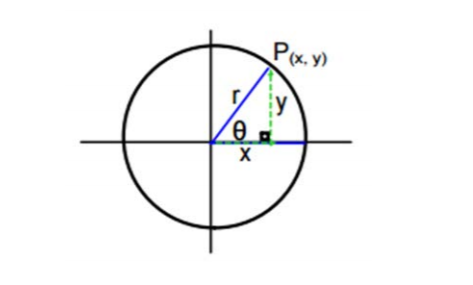
The key component of trigonometry is the 6 trigonometric ratios that relate the sides of a right triangle to the angles
inside of it. A right triangle can be formed on the inside of any circle, where the radius of the circle (r) is also the
hypotenuse (longest side) of the right triangle. The triangle is also formed by the initial side (x), which is a portion
of the radius of the circle located on the initial side of the angle. By Pythagorean Theorem x2+y2=
r2, we can determine the y side of the triangle. Theta (ϑ ) is used to label a non-right angle within the
triangle. The six trigonometric ratio functions are sine, cosine, tangent, secant, cosecant, and cotangent. The ratios of
the six trigonometric functions are explained below (Johnson, 2016).

The trigonometric ratios described how large one side of the triangle is compared to another side. This can all be
determined by a non-right angle inside the triangle. How cool is that?! The angle can also be determined by the ratio of
two sides of the triangle (Johnson, 2016).
The Unit Circle
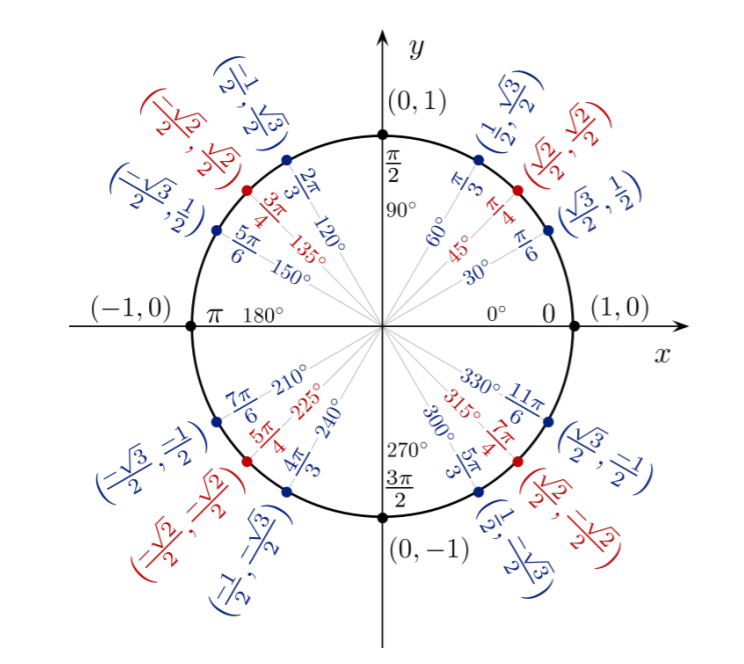
The unit circle is a circle with a radius of one that is centered at the origin of the cartesian coordinate system. It shows
several triangles (that were mentioned earlier) that all have an hypotenuse (r) that is the radius of the circle. The unit
circle relates the sides of the triangles and the angles formed inside the triangle. The point of the triangle that falls on
the circle explains the lengths of the x and y sides of the triangle. Below is a figure of a basic unit circle that shows
several triangles, their side lengths, and the angles inside of them (Johnson, 2016).
Reciprocal Identities
Reciprocal identities relate the six main trig functions and explains how they are all related. The sine and cosecant
functions are just reciprocals of each other. Same with the cosine and secant functions and tangent and cotangent functions.
This makes sense, as the functions all explain the relationships of the lengths of the sides of the triangle (Johnson, 2016).

Quotient Identities
The quotient identities also stem from the unit circle. They explain how tangent and cotangent are related to the sine,
cosine, secant, and cosecant ratios. Since the previous four ratios are all relationships of the adjacent sides or opposite
sides compared to the hypotenuse and the tangent and cotangent are the relationships among the adjacent and opposite sides,
they all can be expressed in one relationship(Johnson, 2016).

Pythagorean Identities
The Pythagorean Identities can be traced back to the Pythagorean Theorem. (Just a reminder that the Pythagorean Theorem
is a2+b2=c2). The Pythagorean Theorem is a relationship of the sides of a right triangle
(sides a, b, and c). Since the trigonometric identities also explain relationships between the sides of a right triangle
and also between the angles in right triangles, the Pythagorean Theorem can be expressed in the following three relationships
using the trigonometric identities (Johnson, 2016).
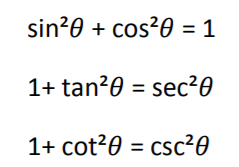
The Complimentary Angle Theorem
The Complementary Angle Theorem shows the relationship between the complementary trigonometric functions. If two acute
angles add up to 90 degrees, then the angles are considered complementary. The Complementary Angle Theorem says that
cofunctions of complementary angles are equal. Thus the following pairs of functions are considered cofunctions (Johnson, 2016).

Sum and Difference Formulas
The sum and difference formulas show the relationship between sums and differences of two angles and the trigonometric
ratios. There are several sum and difference formulas and they can all be traced back to the unit circle and the definitions
of the six trigonometric ratios(Johnson, 2016).
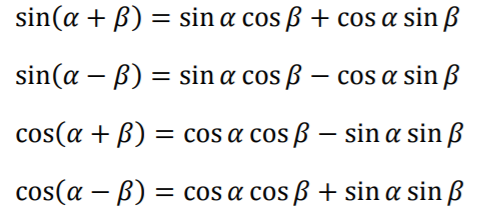
Double and Half Angle Formulas
The double and half angle formulas show the relationships between multiples of angles within a right triangle and the
trigonometric ratios. There are several double and half angle formulas and they can be traced back to the unit circle and
the definitions of the six trigonometric ratios (Johnson, 2016).

Product to Sum Formulas & Sum to Product Formulas
The Product to Sum Formulas & Product to Sum Formulas show the relationships between the trigonometric functions of multiples of two angles and
trigonometric functions of the two angles added together. These formulas also can be traced back to the unit circle and
the definitions of the six trigonometric ratios (Johnson, 2016).
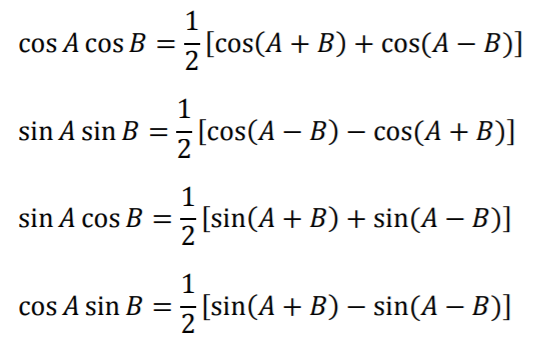
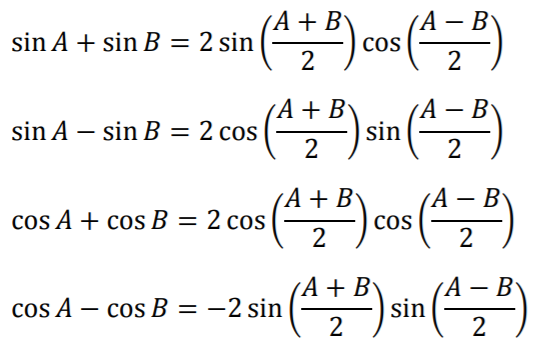
The Law of Sines
The Law of Sines can be used to find all components (all angles and side lengths) of a triangle. The Law of Sines can
only be used when two sets of angles and their opposite side lengths are known. The reason the Law of Sines works is again
because of the unit circle and the definitions of the sine function (Johnson, 2016).
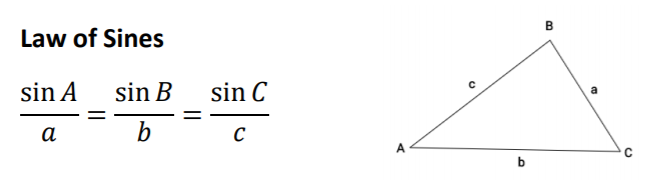
The Law of Cosines
The Law of Cosines can be used to find all the angles of a triangle. It only works if all three sides are known,
and one angle is known. This also works only because of the definition of the cosine function as the ratio of the adjacent
side over the hypotenuse (Johnson, 2016).