Trigonometry is applied to the real world in many ways. Our modern world as we know it, would not be the same if it weren’t for the knowledge and advancements in trigonometry. Although just about anything in our world is affected by trigonometry, just a few examples are listed and explained below.
Measuring Height
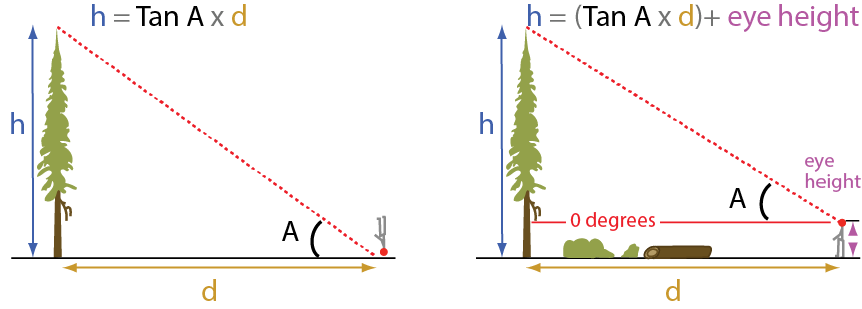
Trigonometry can be used to measure the height of buildings, mountains, and other tall objects. If the distance between
a point and the base of the object is known, along with the angle of depression, the height of the object can be found.
From what was discussed earlier on the explanations page, it is clear to see that if a side length of a triangle and a non-90
degree interior angle is known, trigonometric functions can be used to find the other side lengths. This method is often used
to find the height of mountains and other tall objects that seem out of reach to measure manually. The picture below
illustrates this method, however, often it needs to be taken into consideration the height of the person measuring the
height of the mountain or the height of the equipment recording the measurements. The illustration explains how this is done (Ferrao, 2018).
Flight Engineering
Trigonometry is also used in flight engineering. The following paragraph explains how flight engineering can be broken
down into triangles and how trigonometry can ensure your flight gets to where it needs to go. “Flight engineers have to take
into account their speed, distance, and direction along with the speed and direction of the wind. The wind plays an important
role in how and when a plane will arrive wherever needed this is solved using vectors to create a triangle using trigonometry
to solve. For example, if a plane is travelling at 234 mph, 45 degrees N of E, and there is a wind blowing due south at 20 mph.
Trigonometry will help to solve for that third side of your triangle which will lead the plane in the right direction, the
plane will actually travel with the force of wind added on to its course (Ferrao, 2018).”
Music Production & Theory
Trigonometry also plays a very large role in music production and music theory. All music/sound waves can be modeled
using trigonometric functions and their graphs. An individual note can be modeled with a sine wave while a chord can be
modeled with multiple sine waves. This graphical representation of music and sound can help music engineers in several ways.
First, it allows them to visualize sound. By visualizing the music, they are able to manipulate the notes and chords using
technology to change the pitch and/or quality of the sound. Second, music and sound engineers work in collaboration with
architects to design practice rooms, concert halls, and other rooms where music is performed and practiced. These sine waves
are also taken in consideration in room design. The rooms are designed to ensure that the sine waves don’t bounce (causing an
echo) and also ensuring that they don’t run into each other (causing them to cancel each other out). Sine waves are also
taken into consideration when speakers are being placed - for the same reasons mentioned in the previous sentences ("Trigonometry", 2019).

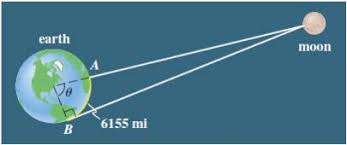
Astronomy
Astronomy is also based off of trigonometry. Trigonometry is used in finding how far away planets and other terrestrial
objects are from the earth. They use trigonometry to find the distance just like it was used to find height at the top of
this page. Using these methods, scientists are also able to find the distance between different terrestrial objects. Without
trigonometry, USA astronauts wouldn’t have been able to get to the moon 50 years ago! Trigonometry was also used anciently to
chart the stars. Angles were used to describe where different stars and planets were located, and how to find them again ("Trigonometry", 2019).