Representations of Fractals
Pure Fractals | Simple Fractals
Many of the most well-known fractals are displayed visually, either in nature or in mathematics. However, fractals can also be mathematical, theoretical, numerical, or descriptive. In this section, we will explore pure fractals and simple fractals.
Pure Fractals
Pure fractals are ones whose iterations go on indefinitely, with never ending iterations of the congruent shapes. Many of the famous fractals are these pure fractals, but often our representations have limits due to technology. The theory or idea behind the fractal, however, can go on infinitely. One example is the Fibonacci spiral. A Fibonacci Spiral is built using squares with side lengths corresponding to numbers from the Fibonacci sequence. Since the sequence is infinite, the spiral too can be infinite. The following applet provides a visualization of the construction of the spiral.
Source: Geogebra applet made by Gretchen Knight
What do you notice about the fractal? I think one of the most notable features is the repeating patterns and iterations: the fractal behavior. Next, I will discuss some more mathematical fractals. These are some of the most common fractal constructions.
Koch Curve and Snowflake: This fractal is constructed by removing the center third of a segment , and replacing it will two segments congruent to the segment that was removed. In effect, you remove a segment and return a triangle. This is then continued through the iterations.
 Koch Snowflake -- Image Source: DataGenetics
Koch Snowflake -- Image Source: DataGenetics
Sierpinski's Triangle and Carpet, and Menger Sponge: This fractal can be constructed using an equilateral triangle or a square. In the case of the triangle, you divide the triangle into four congruent equilateral triangles. You remove the center, then iterate on the remaining three triangles. To make the carpet, you divide a square into nine congruent squares. After removing the center square, you iterate the process on the remaining squares. If you do this process on a cube rather than a square, you end up with the Menger Sponge.
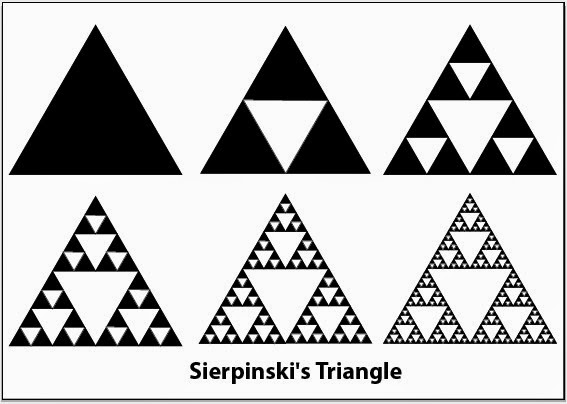 Sierpinski's Triangle -- Image Source: CurseForge
Sierpinski's Triangle -- Image Source: CurseForge
 Sierpinski's Carpet -- Image Source: CurseForge
Sierpinski's Carpet -- Image Source: CurseForge
 Menger Sponge -- Image Source: CurseForge
Menger Sponge -- Image Source: CurseForge
Cantor dust or comb: This fractal is created by removing the middle third of a line segment, then iterating on the remaining segments.

Cantor Set -- Image Source: Wikimedia Commons
Hilbert curve: To construct this fractal, begin with a square that has one side deleted. In the space next to the figure, you copy it, and in the space below, the figure is copied but rotated. Then the figures are connected by line. This process is iterated. The following video illustrates this process in a mesmerizing way.
It's important to note that it's impossible to discuss all possible fractals. However, this is a good starting point to learn, discover, create. Click here to navigate to the References and Resources page which provides applets and websites with many opportunities for discovering, creating, and learning more about fractals.
Next I want to talk about the Julia sets and the Mandelbrot set. The Julia sets were formalized by Gaston Julia, a French mathematician who lived from 1893 until 1978. He served with the French army during World War I, and after suffering a severe injury, he lost his nose. After several unsuccessful surgical attempts to fix his nose, he decided to wear a leather strap over the area instead. Despite being a notable mathematician, hist works were mostly forgotten due to a lack of computing power. That all changed when Benoit Mandelbrot mentioned the Julia sets in his work with fractals and the Mandelbrot set.
 Gustav Herglotz and Gaston Julia via Wikimedia Commons
Gustav Herglotz and Gaston Julia via Wikimedia Commons
In simplicity, the Julia set is constructed as follows. Choose a complex number, z1 = x + yi. Then, zn+1 = zn2 + c, where c is another complex number that is held constant. After many iterations, if the magnitude of z is less than 2, that z is in the set and should be colored accordingly. Repeating this process for varying z1 will yield a fractal shape. If you change c and repeat the process, you will output an entirely different Julia set. Here are graphic representations of several Julia sets.

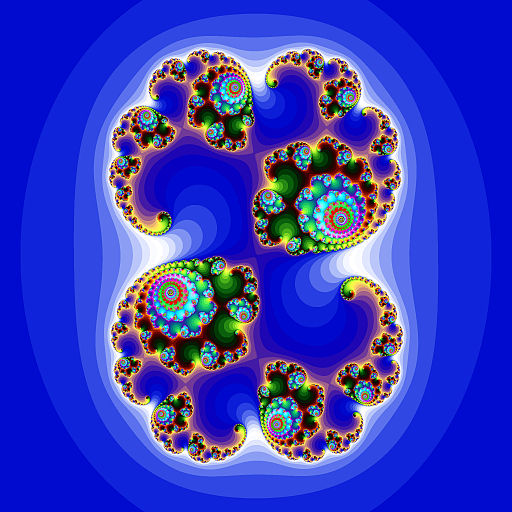
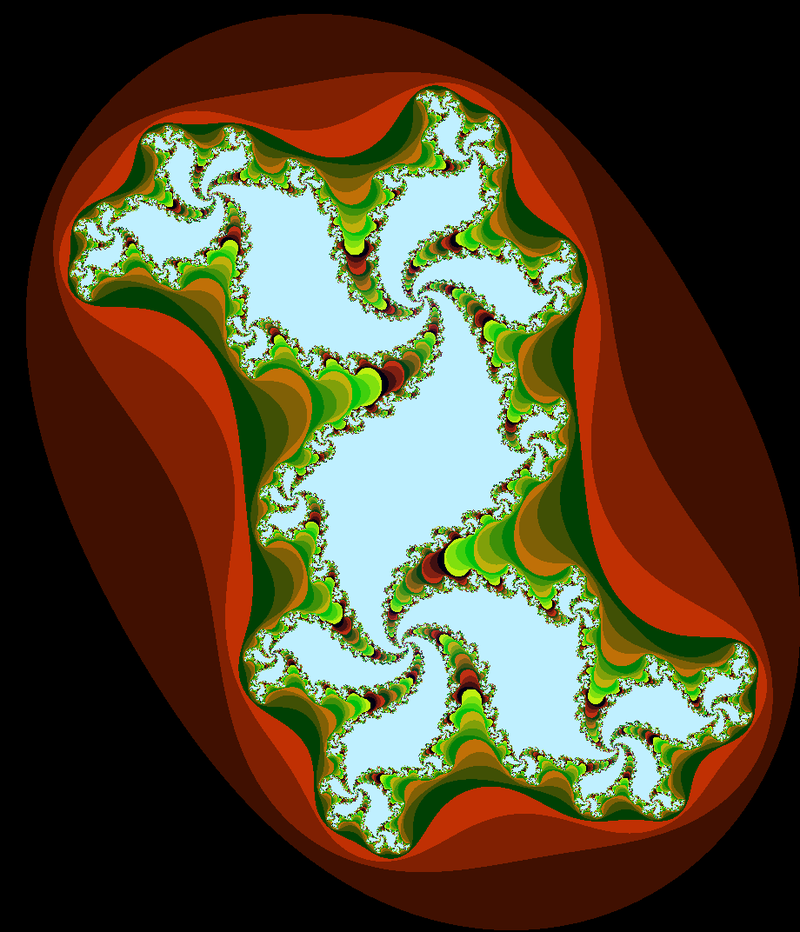

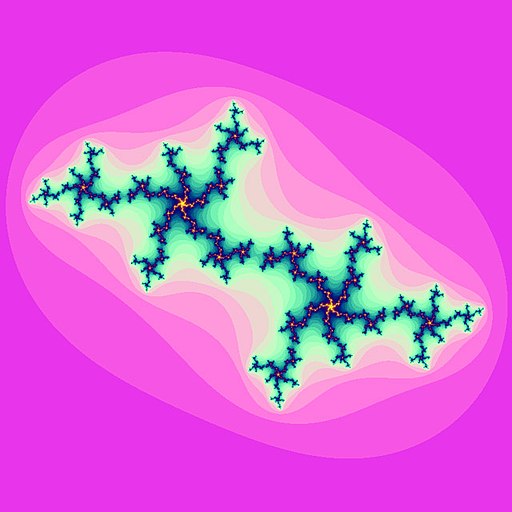



All of these images came from Wikimedia Commons.
The Mandelbrot set is a compilation of all the Julia sets. The Mandelbrot set is generated by calculating z = z2 + c, with a different c for every point z. The coloring in the Mandelbrot and Julia sets is based on whether or not the numbers meet the qualifications. Many representations of Julia sets can be found in the Mandelbrot set by zooming into different points.
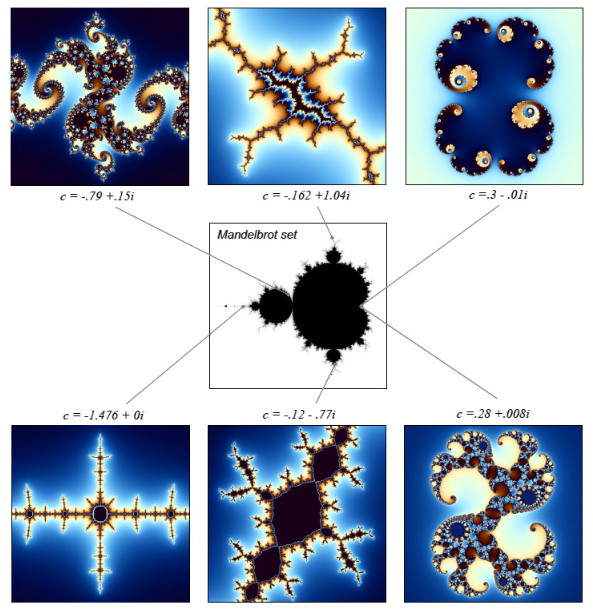 Julia sets at different coordinates from the Mandelbrot set via Karl Sims
Julia sets at different coordinates from the Mandelbrot set via Karl Sims
The following video does a good job at succinctly and clearly explaining how these calculations work and how the Mandelbrot set and Julia sets are related.
If you want to learn more about the Julia and Mandelbrot sets, the following resources are a good starting point.
An explanation by Karl Sims about Julia and Mandelbrot sets
A brief explanation from Wolfram Alpha
A fairly technical article about Julia sets, but still useful information
Top
Simple Fractals
Now let's look at some of the more simple and limited fractals. Many of the fractals that we see in nature or in the world around us are these simple fractals. "Limited fractals don't go on indefinitely; they only display a few iterations of congruent shapes. Simple and limited fractals are also not exact in their self-similarity -- a fern's leaflets may not perfectly mimic the shape of the larger frond . . . While not mathematically exact, they still have a fractal nature" (Haggit). Additionally, in nature and in art, "the number of recursive iterations of each pattern is limited by the scale of the material they were working with." (Haggit)
There are several notable examples of fractals in art. A famous Japanese artist by the name of Katsushika Hokusai lived from 1760 to 1849 in Japan. He is one of the best known artists in Japan, and interestingly, many of his works include fractals. His most famous painting is called Great Wave off Kanawaga. It features waves and foam in repeating sizes.
 Great Wave off Kanagawa -- Image Source: Wikimedia Commons
Great Wave off Kanagawa -- Image Source: Wikimedia Commons
Another example in art are the nesting Russian dolls. While each doll may have different designs on the outside, the dolls are scaled down versions of the original.
 Russian Nesting Dolls -- Image Source: The Russian Store
Russian Nesting Dolls -- Image Source: The Russian Store
I'm nowhere near an expert in art, but finding fractals in art would be another interesting extension to be aware of and to look for.
Finally, many of the limited fractals are found in nature. Listen to the following podcast about various fractals that are found in nature. Additionally, feel free to peruse the pictures below of fractal representations in nature.
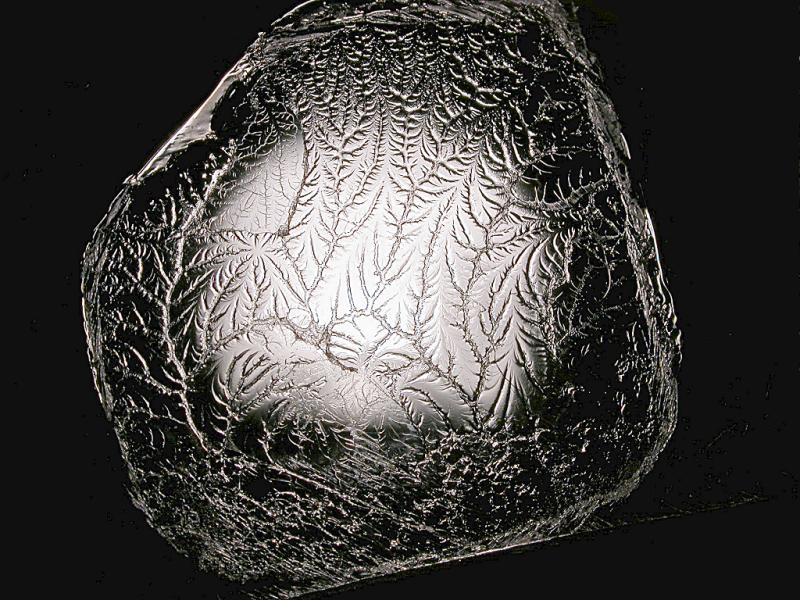 Glue
Glue
 Honey
Honey
 Inlet
Inlet
 Leaf
Leaf
 Lightning
Lightning
 Mountain Terrain
Mountain Terrain
 Romanesco Broccoli
Romanesco Broccoli
 Tree
Tree
All of these images came from Wikimedia Commons.