Exposition of Basic Content
Defining and Clarifying | Characteristics and Description
Defining and Clarifying
At this point you may be asking what a fractal is. Fractals, like many other things, are difficult to concretely define. In the following paragraphs you will find several definitions for fractals, taken from around the web, documentaries, and books. Pay attention to a uniting feature in these definitions, namely that there is an element of self similarity.
Google defines fractals as the following: "a curve or geometric figure, each part of which has the same statistical character as the whole" (Google).
A website called Fractal Foundation provides this explanation. "A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop" (Fractal Foundation)
In his book entitled Chaos, James Gleick gives both of the following descriptions. Mandelbrot's "studies of irregular patterns in natural processes and his exploration of infinitely complex shapes had an intellectual intersection: a quality of self-similarity. Above all, fractal meant self-similar. Self-similarity is symmetry across scale. It implies recursion, pattern inside of pattern" (Gleick, pg 103). Additionally, he says that "the word fractal came to stand for a way of describing, calculating, and thinking about shapes that are irregular, and fragmented, jagged and broken-up -- shapes from the crystal line curves of snowflakes to the discontinuous dusts of galaxies. A fractal curve implies an organizing structure that lies hidden among the hideous complication of such shapes" (Gleick, p. 114).
In a book entitled Fractals: the patterns of chaos, John Briggs offers this exposition. "We will recognize fractal patterns intuitively long before we specify them logically and mathematically. Leaving a definition open is not an unusual procedure in math and science, and seems especially fitting for the idea of the fractal. Not only does such openness allow us to explore the richness of the concept without arbitrary restrictions, it emphasizes the great shift fractal geometry has made away from a strict quantification of nature -- measuring objects and processes in terms of degrees, lengths, and calibrated time durations -- and toward an appreciation of the qualities of nature, such as roughness, openness, branchiness, and roller-coaster rides of 'fractal time.' " (Briggs, p. 71).
And finally, in a PBS Nova feature entitled Fractals: Hunting the Hidden Dimension, Benoit Mandelbrot and other mathematicians discuss fractals. The following is a summary of how they describe fractals in the film. Imagine looking at a complex object, such as a tree, root system, circulatory system. Mandelbrot encourages us to "think not of what you see, but what it took to produce what you see." The documentary continues by saying that it takes endless repetition, and that endless repetition "gives rise to one of the defining characteristics of a fractal: self-similarity." In the film, Mandelbrot describes this further by saying "the main idea is that as you zoom in and zoom out, the object looks the same." It is further described that the whole of the fractal looks just like a part, which looks just like the next smaller part. The similarity keeps on going. This can be recognized as a holistic view. The word holistic is an adjective which is defined as "characterized by comprehension of the parts of something as intimately interconnected and explicable only by reference to the whole" (Google dictionary). Describing objects as fractals gives us a holistic view of the object, rather than attempting to fit classical Euclidean geometry to objects that aren't "classical" at all.
Top
Characteristics and Description
That was a lot of information with varying ideas and viewpoints, but hopefully now the idea of fractals has become a little more clear. Now, let's highlight some of the common characteristics of fractals as well as the main way we describe fractals.
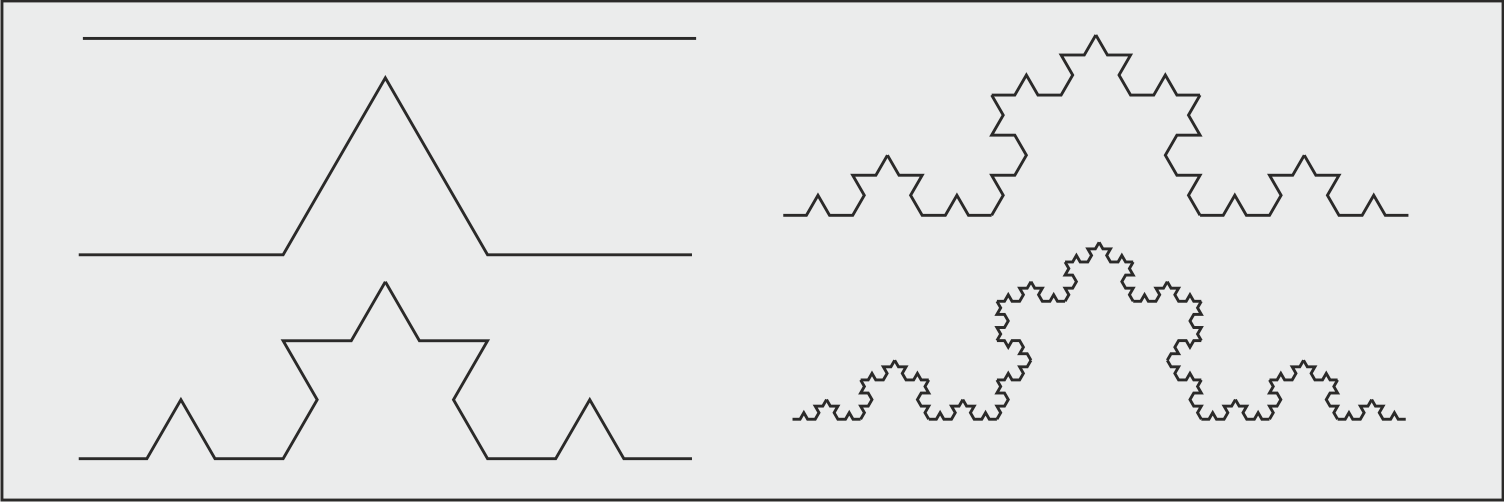
Fractals have an element of self-similarity, meaning that they look similar, no matter how zoomed in or out you are. This self-similarity can be counted, inspected, and/or defined for the fractal. If an object has an aspect of self-similarity across scales, it can probably be considered a fractal. The following graphic further describes this process.
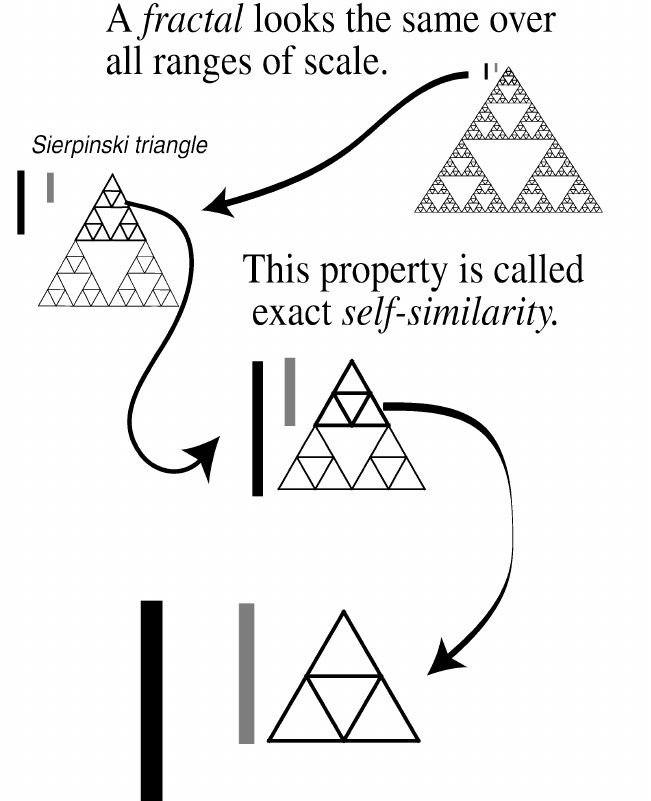 via Research Gate from Carl Anderson
via Research Gate from Carl Anderson
Another important aspect is that of iterative patterns or feedback loops. An iterative pattern involves doing a procedure, transformation, or calculation. From that, you take the result, and repeat the same process, over and over again. It is essentially a "rinse and repeat" process. A couple examples of iterative include the Fibonacci sequence and Sierpinski's triangle. In the Fibonacci sequence, you add the two prior numbers to get the new one, described by the formula fn = fn-2 + fn-1 , where f0 = 0 and f1 = 1. Here is the first few digits of the sequence: 0, 1, 1, 2, 3, 5, 8, 13… To construct Sierpinski's triangle, divide an equilateral triangle into four congruent equilateral triangles. Delete the center triangle. For each remaining triangle, divide it into four congruent triangles and delete the center. Use the following applet to examine that process more.
Source: Geogebra applet made by Gretchen Knight
The last characteristic of fractals to discuss is the fractal dimension. Think about a few basic elements from classical geometry - namely a line, a square, and a cube. A line has one dimension, a square has two dimensions, and a cube has three dimensions. Computations involving these elements are fairly straight forward. You can calculate the length of a line, the area of a square, and the volume of a cube. Consider now a fractal. For some fractals, these typical calculations don't make sense. The a fractal will often will up more space than a line, but less space than a square (or other 2 dimensional shapes). For fractals, we can calculate the fractal dimension. This involves identifying N, the number of self similar pieces, and S, the scale factor. Self-Similar Pieces (N) are defined as the number of objects in the figure that are the same size and shape (i.e. the number of times the previous iteration appears in the figure). Scale Factor (S) is the scale from one iteration to the next (i.e. how does the length of each object compare to the previous).
In the above graphic, N = 4. In the progression from left to right, you can see that each line segment is replaced with four smaller segments that are of equal length to each other. Additionally, S = 3. One of the original segments can be replaced by three of the new smaller segments. Once you identify N and S, the calculation for dimension is simple. D = log(N)/log(S). This equation is related to N = SD.
Use the following applets to explore and learn more about the fractal dimension. First, examine and explore the line, square, and cube to get familiar with N and S.
Complete this table using the information you found above. Continue to identify N and S for Sierpinski's triangle and Koch's curve.
Use the applet below to calculate the dimension for the various objects, and see how dimension is related to N and S (self similarity and scale factor). What does the dimension of an object tell us?
The dimension of a fractal describes its overall roughness. This degree of irregularity "corresponds to the efficiency of an object in taking up space" (Gleick, p. 102). Consider a Koch curve. The curve fills more space than a line does, but less than a plane. It's more than one dimensions, yet less than two. The fractal dimension gives a description of this amount of space that is filled.
Thinking again about the coast of England example, it may be impossible to exactly calculate how long the coast is, but using the fractal dimension we can describe the roughness. This is still important information. Additionally, the degree of irregularity, or roughness, is constant over scales. No matter how far in or out you are zoomed on a fractal, the fractal dimension will remain the same. Hence, this is why the fractal dimension is one of the best ways to describe a fractal.