Explanation of Mathematics for Circles
Knowing the parts of a circle is useful in order to make circles useful to solving problems. The parts of a circle this paper is going to focus on are center, radius, chord, diameter, secant, tangent, point of tangency, arc, circumference, semicircle, and sector. They all play important roles when defining different areas or looks about circles. These different parts are defined in the video I made along with pictures to better visualize. Here is the link if you wish to better understand Parts of a Circle. These parts are used to help when solving problems.
Not only are there different parts of a circle there are also different angles formed from the parts of a circle. The different types of angles are central, inscribed, interior, and exterior angles. A central angle is formed from two radii to the center of a circle. The inscribed angle has its vertex on the circumference of the circle with two chords forming the angle. Interior angles are formed on the inside of a circle when two chords cross each other. The exterior angle is formed when the vertex of an angle it on the outside of a circle and the rays of the angle touch at least one point on the circumference. All of these angles form different theorems to help with solving problems.
Figure 1 gives some theorems about how to find the angle given the measure of the arc. These
relationships are a big deal. The paper will go into more why this is later on. Also if we were
given the angle but want to find the measure of the arc the table is still helpful. The only thing
needed is to manipulate the equation, so the arc is by itself. Understanding these theorems can be very
insightful and helpful.

When using circles to solve problems people can either use degrees or radians for the angle. Both of
these units are very useful tools and depending on the problem one may be more helpful over another.
In this paper will focus more on degrees. Consider an approach to angle measure that defines degrees as
the standard unit of angle measure and asks students to use a protractor to assign degree measures to angles
(Moore, 2013). All this quote is saying is that a degree is a unit of measurement. There is not a difference
between radians and degrees in the sense that both are a unit of measurement. If this is understood then maybe
when changing between these two methods wouldn't be so hard to comprehend.
When someone says the word circle, a common thought is $\pi r^2$ This expression represents the area of a circle with a given radius. Another common expression is $2\pi r$ which is the circumference of a circle. Those two expressions are taught in elementary years and carried on through the years. We are going to talk more about the mathematics behind finding the arc length of a circle.
If the angle of a circle is given at the center then the equation for the arc can be found by thinking of the
equation of the circumference. The only thing also needing to be included is the angle. The way to find the arc
length would be Arc length $=2\pi r \frac{\theta}{360}=r\theta \frac{\pi}{180}$ if we are using degrees. The original
formula is written in radians so to convert it into degrees the angle is multiplied by $\frac{\pi}{180}$. Because the
formal equation written in radians to find arc length is Arc length $=r\theta$. This makes sense because of the
relationship between angles and arcs. The bigger the angle the bigger the arc is going to be and the same
with the radius the bigger the radius the bigger the arc. Understanding having to change degrees to
radians is important. This is because if on would like to use Figure 1 table then one must multiply the
angle by $\frac{\pi}{180}$.
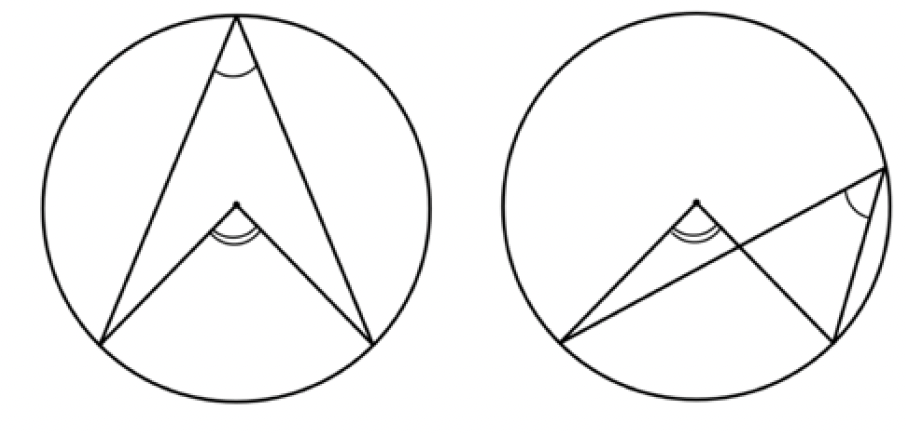
Now let's look at the relationship between the center and inscribed angles. If the chords intersect the points
the radii intersect the circumference, then it doesn't matter where the vertex of the inscribed angle is as long
the vertex isn't on the arc the center circle is measuring. Figure 2 shows this and how they show the same thing.
Kawan and authors explain Figure 2, Even though both figures demonstrate the angles at the centre and at the
circumference of the circles subtended by the same arc, some students do not realize that these figures are related
to the same property of a circle
(Kawan, 2018). The applet below allows you play around with this property.
Both the applet and the figure 2 show that the inscribed angle is half the size of the centre angle. This relationship makes it so that so many other things can be solved. It explains the equation from Figure 1. When rearranged and putting it into degrees we get the equation Arc length $=2r\theta \frac{\pi}{180}$.