The Pythagoreans might have gotten a little carried away with their interpretations of Pythagoras’ findings. However, one important truth has been learned: harmony is derived from proportions. Let’s take Pythagoras’ ideas and expand upon them.
As Pythagoras has already told us, 2:1 gives us an octave, 3:2 gives us a fifth, and 4:3 gives us a fourth. Using ratio multiplication, we can show that a fifth and a fourth combine to make an octave (3:2*4:3=2:1). Knowing that we can perform algebraic operations on the ratios while maintaining their musically theoretical implications opens a whole new world. Now, we can define the difference between a fifth and a fourth (3:2/4:3=9:8), called a whole tone. Since we know an octave can be broken into a fifth and a fourth, and that there exists a whole tone between a fifth and a fourth, we can rewrite a fifth as a fourth plus a whole tone. So, we now have that a fourth plus a whole tone plus another fourth equals an octave. At this point, we are defining a whole tone as the smallest relevant division of the octave. Due to this, it is logical to attempt to keep breaking down a fourth until it’s merely a component of whole tones. However, when we compute this algebra, the numbers don’t add up.
Based on what we’ve already discovered, it would be reasonable to believe that a whole tone plus a whole tone would be the same as a fourth minus a whole tone. We can see that a whole tone plus a whole tone (9:8*9:8) gives us a ratio of 81:64 while a fourth minus a whole tone (4:3/9:8) gives us a ratio of 32:27. Why are these ratios not the same? That’s because of a distinguishment Pythagoras discovered: a major third versus a minor third. Combining two whole tones together create what he penned as a major third, while a fourth minus a whole tone would be called a minor third, because a minor third is a smaller value than of a major third. This leads us to an issue then: a major third plus another whole tone (81:64*9:8=729:512) does not equal a fourth (4:3). This is how Pythagoras created something called a halftone. If we take the difference between the fourth and the major third (4:3/81:64), we get a ratio of 256:243. Upon inspection, we can see that 256:243 is smaller than 9:8. In other words, a fourth is comprised of two whole tones plus some tone even smaller than a whole tone. However, if we think about this in even different terms, we can discover something interesting about the halftone:
4th = 2(whole) + half
So, 4th + 4th = 4(whole) + 2(half)
4th + 4th = 4:3*4:3 = 16:9
4(whole) + 2(half) = 9:8*9:8*9:8*9:8*256:243*256:243 = 16:9
However, 5(whole) = 9:8*9:8*9:8*9:8*9:8 = 16:9 as well.
So, if 16:9 = 4(whole) + 2(half) and 16:9 = 5(whole),
Then whole = 2(half)
We can now see that a halftone is half the value of a whole tone (hence the name halftone). Since we established that an octave can be broken up into a fourth plus a whole tone plus another fourth, we now know that an octave can be further broken down into the summation of a whole tone, a whole tone, a halftone, a whole tone, a whole tone, a whole tone, and a half tone. Though these 7 tones can be arranged in any order and still maintain the same proportion of an octave, this particular arrangement of whole tones and halftones is called the major scale. Below is a diagram of the Pythagorean creation of the major scale:
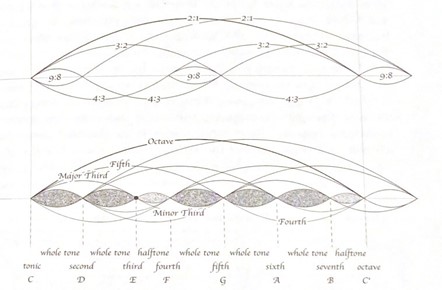
Looking at this diagram, it now becomes obvious why things received the names they did: a fourth is the interval between the starting note and the fourth note of the scale, a fifth is the interval between the starting note and the fifth note of the scale, and an octave is the interval between the starting note and the 8th note of the scale/the same note but double the pitch.
To better understand the mathematical implications of intervals, the following applet demonstrates the relationships between two different sound waves: