The Birthday Problem

If the answer to the birthday problem is counterintuitively 23 people, what mathematical calculations make that true? It all comes down to a few rules of probability. In this problem, we are considering a question asking for the probability that "at least two people share a birthday." Calculating a probability of "at least ____" can be computationally intensive because there are so many cases to consider. For example, if at least two people share a birthday, any number of two or more people could share a birthday (e.g. 2, 3, 50, or 100 people in a room could share a birthday). Theoretically, there could be an infinite number of people in a room, making the probability nearly impossible to calculate directly. This is why an "at least" probability is often best calculated using what is called the complement rule because it can make complex probabilities easier to find (Schneiter, 2020). The complement rule is defined as P(A) = 1-P(A'), which means the probability of an event occurring is equal to 1 minus the probability of the opposite event occurring. This is based on the concept that the total probability of mutually exclusive outcomes sums to 100% or 1 when written as a decimal.

For example, there is a 100% chance that a coin will read either heads or tails when flipped. Let H denote that the coin reads heads and T denote that the coin reads tails. If we were to flip a coin 3 times these are the possible outcomes: HHH, HHT, HTH, THH, TTH, THT, HTT, TTT. If we wanted to find the probability of getting at least 1 head in 3 coin flips, we would have to consider the total probability of the first seven outcomes in the list above because all of them contain at least one head. To calculate this directly looks like:

P(at least one head flipped in 3 tosses) = P(HHH) + P(HHT) + P(HTH) + P(THH) + P(TTH) + P(THT) + P(HTT) + P(TTT) = 1/8 + 1/8 + 1/8 + 1/8 + 1/ 8 + 1/8 + 1/8 = 7/8.

That is quite a lot of computation considering that we only have seven possible outcomes in this case. With the birthday problem, there are nearly infinite outcomes, making a direct calculation like this one nearly impossible. However, applying the complement rule, we can consider the following:

P(at least one head flipped in 3 tosses) = 1- P(TTT) = 1 - 1/8 = 7/8.

Using the complement rule allowed us to get the same result much more directly by subtracting the probability of the opposite event occurring from the total probability of 1 (Schneiter & Partridge, 2020).

Applying this to our original problem, we want to consider the opposite event of "at least two people [sharing] a birthday." If at least two people share a birthday, this implies at least one pair of people share a birthday, meaning the opposite of this event would be no one sharing a birthday. Therefore, using the complement rule, we can say:

P(at least two people in the room share a birthday) = 1-P(no one in the room shares a birthday).

What we are left to find is the probability that no one in the room shares a birthday. To keep the math simple, we will ignore leap years and assume that the birthdays of everyone in the room are independent (e.g. no twins, etc.). Calculating this probability involves applying the multiplication principle because we first choose a person, then consider the probability that a second person does not have the same birthday as the first AND a third person does not have the same birthday as the first or the second AND so on until we have obtained our desired probability of about 0.5. When we are finding the probability of a string of events happening at the same time (those ANDs), the multiplication principle tells us that we will multiply the individual probabilities together. In our case this looks like the following:

P(no one in the room shares a birthday) = (365/365) * (364/365) * (363/365) ... *(365-n/365) (where n is the number of people in the room).

Therefore, we can apply the complement rule to get:

P(at least two people in the room share a birthday) = 1 - (365/365) * (364/365) * (363/365) * ... (365-n/365).

Recall that our original question wanted to have the above probability be at least 50%. Originally, this would have been done through trial and error by hand, but now we are able to use tools like the following applet created by Kady Schneiter to recognize these probabilities quickly.

As the slider is moved to increase n, we see that the probability of at least two people in a room sharing a birthday is 0.5073 or just over 50% when there are 23 people in the room. Hence,

0.5073 = 1 - (365/365) * (364/365) * (363/365)* ... (365-23/365).

An extension for the traditional birthday problem we could consider is: "How many people would need to be in a room for there to be a 98% chance that at least two people share a birthday?" Applying what was discussed above, we could use the applet to see that:

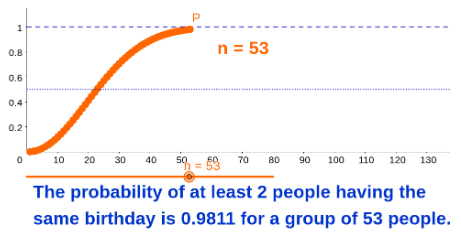
This would be calculated as follows:

0.9811 = 1 - (365/365) * (364/365) * (363/365)* ... (365-53/365).

Therefore, if there are 53 people in a room, there is a 98% chance that at least two of them share a birthday. With this in mind, it is very likely at least one pair of people in most college classes share a birthday!

One thing that is important to keep in mind is the difference between the probability that at least two people in a room share a birthday and the probability that someone in the room shares a birthday with a specific person. An example of this would be if you wanted to know how many people would need to be in a room for the probability that you share a birthday with someone to be 50%. To calculate this we would again apply the complement rule as we did in the previous situation. Now, instead of the opposite event being "no one shares a birthday" it will be "no one shares a birthday with a specific person" as follows:

P(At least one person shares a birthday with a specific person) = 1 - P(No one shares a birthday with a specific person)

= 1 - (364/365)*(364/365)*(364/365)*...(repeated n times)

= 1 - (364/365)ⁿ.

Using the following applet that applies the above formula, we can see the probability that there is someone in a room that shares a birthday with a specific person depending on the number of people in the room.

From the above applet, we can see that there is a 50% chance someone in a room shares a birthday with a specific person when there are 253 people in the room.