My Project Webpage


Applets Video Resources/Links
History and Background Mathematical Explanation Significance and Application
Home



About my project:

Most students at this point probably already recognize what a factorial is, and how it is applied in mathematics. But many have failed to think deeper into the subject. With a concept as seemingly simple as factorials, it begs the question; have you ever thought deeper into what their real-life applications are? For example, how many ways can you organize a deck of cards? This may be trivial to some, but how big is this number when quantifying it using tangible objects? This article will dive deeper into understanding the history, nuances, applications, and quantification of factorials.








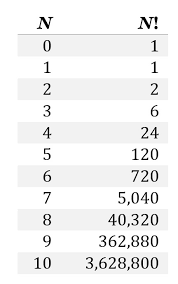
Here is a quote from the cuemath website reguardinng the history of factorials:

"In the year 1677, Fabian Stedman, a British author, defined factorial as an equivalent of change ringing. Change ringing was a part of the musical performance where the musicians would ring multiple tuned bells. And it was in the year 1808, when a mathematician from France, Christian Kramp, came up with the symbol for factorial: n!. The study of factorials is at the root of several topics in mathematics, such as the number theory, algebra, geometry, probability, statistics, graph theory, and discrete mathematics, etc."




References