Project
A major application of pi is that it is essential in finding areas and volumes.
The area of a circle is given by the equation \(A=\pi r^2\). We will explore why this is.
From the drawing below we see that a circle can be partitioned into many isosceles
triangle-shaped sections. Since the sides that are congruent go from the center
point of the circle to the outer edge, by the definition of a circle, each side
of the triangle has a side length of r. As the number of triangles increases,
the triangles become smaller and they can be arranged into a parallelogram. The
height of this parallelogram is the length of one of the sides of the triangle,
which is r. The length of this parallelogram is one half of the circumference of
the circle. The circumference of the circle is \(2\pi r\), thus one half of the
circumference is \(\pi r\). Thus the area of this parallelogram, which is the area of the
circle rearranged, is \(\pi r\cdot r\), or \(\pi r^2\) (Cuemath).
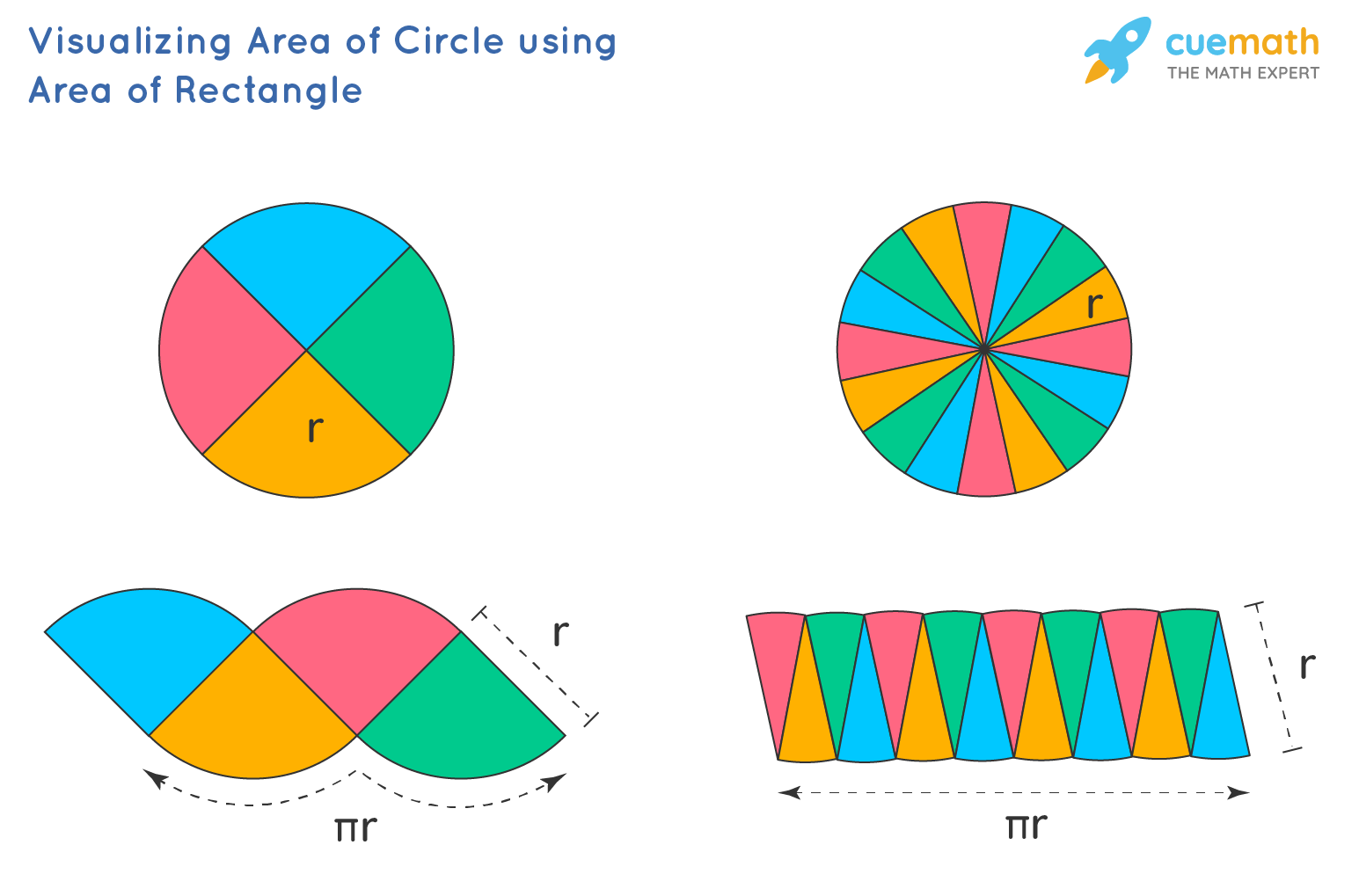
Image from Cuemath
Since pi is essential in finding the area of a circle, it is also fundamental in
finding the surface area of shapes containing circles, such as cylinders and cones.
It is also essential in finding the volumes of these shapes. The formulas for all
of these surface areas and volumes include pi (Mometrix).
While being able to calculate the surface area and volumes of three dimensional
shapes is very useful for your geometry test, it begs the question- when is this
applicable in real life? The answer is that it is applicable more often than you
might initially think. Surface area and volume are used in everyday life: how much
wrapping paper it takes to wrap a present, how much paint to use, how much liquid
is needed to fill a container. There are also many practical applications for
these concepts in construction and engineering, and even in rocket ships. In
fact, NASA has an entire webpage dedicated to how pi is used in their work. Pi
is used to determine the volume, surface area, and density of planets. Once
scientists have determined the density of planets, they are able to determine
which materials the planet is made of. Scientists also use pi to study craters.
They work to determine how circular a given crater is using pi and the crater's
perimeter and area. From these calculations, "planetary geologists can reveal
clues about how the crater was formed and the surface that was impacted." Pi
is essential in finding surface area and volumes and therefore understanding
the universe around us (NASA).
Curious? To check out many of the ways that NASA uses pi, click here!

Another application of pi is converting radians to degrees. Most high school
students learn how to convert radians to degrees and vice versa by using the
conversion factor of \(180= \pi\) radians. However, what most high school students do not
learn is why that is and why radians are useful. "A radian is defined as an arc
that has the same measure as the radius of a circle" (Mometrix). We know from the
definition of pi that \(\pi=\frac{c}{d}\), which can be rearranged to show that the circumference
of a circle is given by \(C=\pi d\). We also know that \(d=2 r\) where r is the radius. So by
substitution we can find that \(C=2\pi r\) and so the measure of the entire circle is \(2\pi \)
radians. The measure of an entire circle is also defined to be 360 degrees, and
so \(360=2\pi \) radians. It is from this relationship that we get the conversion factor
most commonly used: \(180=\pi\) radians. Knowing where this relationship comes from makes
the conversion factor much more intuitive.
Check out this visual of radians vs. degrees!
Applet by Robert Radu and Soongy found on Geogebra
Radians are significant because they have meaning. Degree is a measure that is
arbitrarily assigned- different societies have chosen \(400^\circ\) as the measure of a
circle or \(200^\circ\) as the measure of a circle. The only meaning that a degree has is
an amount that is arbitrarily assigned to it. In contrast, radians have meaning
inherent in their definition and structure. A circle will always be exactly \(2\pi \)
radians. In addition, if the circle is a unit circle then the length of the arc
subtended by the central angle of the circle is the radian measure of the angle.
Radians are useful in calculus and in trigonometry. Graphs of sine and cosine are
much easier to make sense of if they are done using radians rather than degrees.
If degrees are used for these graphs, the horizontal axis has to be stretched to be
able to see the typical curve for a sine or cosine graph, whereas a typical graph
with both the horizontal and vertical axes scaled the same functions well for
radians. Radians are more useful for calculus as well because their derivatives
work out much nicer, whereas if degrees are used there will always be a multiplier
of 180 complicating the equations (McMullin).
Image courtesy of Google Images
Another application of pi is closely connected to radians as well as sine
functions- waves. Waves are described using radians, and thus pi. The function for
the period of a wave is T= Period = \(\frac{2\pi}{k}\) where k is the angular frequency. This
equation is one that most physics students memorize. However, what many students
may not realize is that this equation is derived from the relationship of pi and
radians. Since one circle is complete in \(2\pi\) radians, it is also true that a full
cycle of the wave is completed at \(2\pi\) radians, and thus a sine or cosine wave has
a period of \(2\pi\) radians. It is possible to parameterize and understand waves
because of our understanding of pi.


