For over 2,000 years mathematicians have been studying regular polyhedra which has played a vital role in the development of Western science and philosophy. Plato's ideas on regular polyhedra influenced later ideas about cosmology. Kepler's foundational discoveries in astronomy were inspired by Pythagorean-Platonic ideas about the significance of geometry in the universe. Platonic geometry is also a prominent part of the work by an American inventor and philosopher named R. Buckminster Fuller. He created complex sculptures and designs to experiment with structural innovation. The sculptures were models of the geometric properties behind its construction (Heinz).
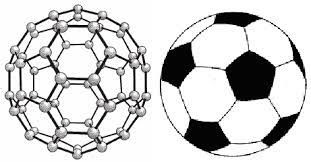
Other applications of regular polyhedra are found in science and engineering. In science there are many viruses, organisms, and bacteria that are shaped as icosahedron. The use of polyhedra has allowed accurate visual representations of these organisms. The geometry of polyhedra has allowed for a better understanding of the structure and the nature of the organisms and the way that they interact with their surroundings. "Viruses, for example, must enclose their genetic material inside a shell of many identical protein units. The icosahedron is the most efficient way to do this, because it consists of a few regular elements but is almost shaped like a sphere"(Mathigon). In addition to being shaped like an icosahedron, many molecules are shaped like regular polyhedra. The one that is most well-known is C-60 (shown in the figure above), it is a molecule that has 60 carbon atoms that arrange in the shape of a truncated icosahedron. Crystal atoms are arranged in a grid that consists of tetrahedra, octahedra, or cubes. Polyhedra have enhanced the understanding of the inner workings of the microscopic world (Mathigon).

Octahedra and Tetrahedra are very stable and rigid, so they are often used in construction. In architecture they use space frames which are polygonal structures of regular polyhedra that can support an incredible amount of weight. This geometry has allowed architects to design more stable and unique structures than they could before polyhedra were utilized. Another well-known application of polyhedra is a soccer ball, which is not a true sphere but a truncated icosahedron. The Platonic solids are also used in the creation of dice; the symmetrical nature of dice makes them more fair in games of chance (Mathigon).
The recognition of polyhedra occurred in ancient times. As polyhedra have been studied and defined, the precise mathematical geometry of these shapes has gradually changed the way that humans interact with and understand the world. This unique subset of three dimensional shapes is present in nature and on microscopic levels. A deeper understanding of polyhedra exposes the logical geometry of the world around us and provides new avenues for research, development, and discovery.