Regular and semi-regular polyhedra are supported by in-depth mathematics. To really understand the math behind polyhedra, there must be an understanding of the definition of each type of polyhedron. A regular polyhedron is a solid figure with all of the faces being congruent regular polygons, with the same number of polygons being around each vertex. A semi-regular polyhedron is a solid figure where each of the faces is a regular polygon but the faces are not congruent. The symmetry group must also be transitive on its vertices. There are a distinct number of possible regular and semi-regular polyhedra.
Use the sliders to view the nets of each different polyhedron.
Press the Animation! button to see all of the nets unfold at the same time.
There are only five regular polyhedra possible: tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The reason why there are only five possibilities has to do with the angles in the solids at each vertex (Vidermanova & Klepancova). There are two requirements for a regular polyhedron: each of the vertices must be a vertex for at least three faces, and the total angle measurement at each vertex between all of the faces must be less than 360 degrees. Understanding the Triangle Sum Theorem is vital to determining whether a polyhedron is regular or not. The Triangle Sum Theorem states that the sum of the three interior angles in a triangle is always 180 degrees. Knowing that theorem makes it easier to find the angles at each vertex of a polygon. If the angles at a vertex add up to 360 degrees or more they would create a flat surface or a negative curvature which would not result in a solid (Weisstein).
The value of the angle that is less than 360 degrees is known as the angle defect. There can not be a regular polygon that has six or more sides since they would have angle values of 120 degrees or more. Therefore that leaves you with a polygon with five sides (pentagon), four sides (square), and three sides (triangle). In a pentagon each vertex is 108 degrees, so there can only be three faces at a vertex or else it would exceed 360 degrees. This is similar to a square; each vertex is 90 degrees, so there can only be three faces at a vertex. In a triangle each vertex is 60 degrees and there can be three, four, or five triangles at a vertex before it would exceed 360 degrees. A tetrahedron is created with three triangles at a vertex; the angles at the vertex add up to 180 degrees. An octahedron is created by four triangles at a vertex; the angles at the vertex add up to 240 degrees. An icosahedron is created by five triangles at a vertex; the angles at the vertex add up to 300 degrees. These are the five possible polyhedra; the one with pentagonal faces (dodecahedron), the one with square faces (cube), and the three with triangular faces (tetrahedron, octahedron, and icosahedron)(Weisstein).
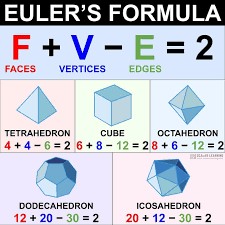
As stated previously, Euler's formula (V+F-E=2) was a vital part of understanding polyhedra. "Euler's formula can be viewed as the catalyst for a whole new way of thinking about shape and space"(Kirk). The sides of a polyhedron are considered faces, the sides of the faces are considered edges, and the corners of the faces are vertices. To understand what Euler's formula shows, look at a regular polyhedron such as the cube. The cube has eight vertices: V=8, twelve edges: E=12, and six faces: F=6. Plugging those values into Euler's formula gives you V - E + F = 8 - 12 + 6 = 14 - 12 = 2, which is what Euler's formula shows it should be. This formula works for each regular polyhedron. It can also be used to see that there is no simple polyhedron with exactly seven edges or ten faces or seventeen vertices. It is a simple way to show that the polyhedron is regular. Euler's formula led to the discovery of the Platonic solids. Mathematicians have discovered that all solids in three-dimensional space are characterized by the number of holes they contain. Euler's formula does not work for polyhedra with holes, but mathematicians have found a formula derived from Euler's formula that works. "For any polyhedron, V - E + F is exactly 2 minus 2 times the number of holes! It turns out that this number, called the Euler characteristic, is crucial to the study of all three-dimensional surfaces, not just polyhedra"(Kirk).
Semi-regular polyhedra can be separated into three types: prisms, antiprisms, and the Archimedean solids. There are an infinite number of prisms and antiprisms possible but only thirteen Archimedean solids. Prisms have the same regular polygon on top and bottom and straight lines that join the vertices to form square sides. Antiprisms have the same regular polygon on the top and bottom but are turned so each vertex of one of the polygons is joined to two vertices of the other, so it forms an equilateral triangle. Prisms and antiprisms do not meet the requirements to be an Archimedean solid. 
The two requirements of semi-regular polyhedra are that they have to have the same arrangement of polygons at each vertex and each vertex cannot have an angle exceeding 360 degrees. The Archimedean solids can be created by truncating, expanding, and moving the faces. Five of the polyhedra are created by truncating (cutting off the corners) of the regular platonic solids: truncated tetrahedron, truncated cube, truncated octahedron, truncated dodecahedron, and the truncated icosahedron. The remaining solids are the snub cube, snub dodecahedron, cuboctahedron, rhombicuboctahedron, truncated cuboctahedron, icosidodecahedron, rhombicosidodecahedron, and truncated icosidodecahedron (Anderson).
Explore the Prezi below to learn more about Platonic and Archimedean Solids.