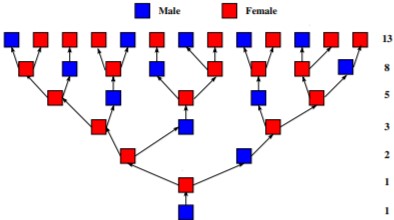
Fibonacci first introduced his special recursive sequence by posing a question about rabbit reproduction (Scott p. 1). He hypothesized that the rabbits reproduced each month according to the prior months, which resulted in the values for the Fibonacci sequence (Katyal, p. 3). Ironically, the breeding of rabbits does not follow the Fibonacci sequence, however, some reproductive models follow the Fibonacci sequence naturally. The reproduction of bees are one example of the Fibonacci sequence. A male bee, also known as a drone, comes from an unfertilized egg laid by the queen bee while the female bee comes from the fertilized egg (Scott, p. 10). Therefore, every male has one parent, and every female has two parents. When tracing the lineage of a male drone we start to see how each iteration of the drone’s ancestors matches up with the Fibonacci sequence. The lineage for a female bee also follows the Fibonacci sequence, however, its initial values are shifted (Scott, p. 11). Refer to Figure 4 for a depiction of the drone’s lineage, as well as the queen/female bees. The image in Figure 4 shows that starting with one drone bee for the first generation, requires a female bee as the only parent in the first generation. Thus a female bee requires both a drone and a female bee for parents, so two generations back the original drone bee has 2 ancestors. To go back another generation, we get that there are three additional ancestors as one comes from the drone and two from the female. The population of a bee colony also relates to the golden ratio, where the ratio between the number of females to male bees in a colony is φ:1 (Ilić, p. 126).

| Generation | Drone | Worker/Queen |
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 3 | 3 | 5 |
| 4 | 5 | 8 |
| 5 | 8 | 13 |
| 6 | 13 | 21 |
| 7 | 21 | 34 |
| 8 | 34 | 55 |
| 9 | 55 | 89 |
Figure 4: Lineage of Bees
Another natural occurrence of the golden ratio appears in the lungs of mammals.
The lungs are made up of a bronchial tree, where a bronchus splits into two bronchioles of different lengths.
For every two bronchioles, they share a ratio that is approximately equal to the golden ratio (Katyal, p. 6).
This approximation has helped biological engineers develop ventilators.
The lungs aren’t the only part of the human body that we see the golden ratio in.
When studying a healthy heart, the ratio between the left ventricle transverse and the vertical measurement of the heart resulted in a convergent value of 1.618, the golden ratio (Ilić, p. 127).
The study also noted that people with heart failure typically had either a ratio of 1.64 (mild heart failure) or 1.4 (terminal heart failure) instead of φ (Ilić, p. 127).
They have been able to make predictions based on the golden ratio to determine the healthiness of the heart (Ilić, p. 128).
Another interesting study identified a relationship with the heartbeat converging to φ and feeling peace and tranquility (Kazemi, p. 1).

Figure 5: Proportion of the Human Arm
The human arm also has a proportional relationship that is similar to the golden spiral, going from the tip of the middle finger to the wrist and from the wrist to the elbow (Katyal, p. 7). See Figure 5 above if you are interested in testing this ratio.
Nature is also full of golden spirals; for example, pinecones, sunflowers, and pineapples all contain the golden spiral in their structure (Kazemi, p. 1).

Figure 6: Spirals on a Pinecone

Figure 7: Spirals on a Sunflower (left) and Pineapple (right)
Each of these naturally occuring objects have a spiral that expands clockwise, and a spiral that expands counterclockwise as pictured in Figures 6 and 7. In the applet below, the spirals are made by the number of sunflower seeds and the proportion of degrees in a circle (r). Explore how the spiral changes as r changes, and which spiral is the most compact with seeds. The space utilized by the seeds is maximized to produce the highest number of seeds possible in as little space as possible. The newest grown seed has a position that depends on the previously grown seed (Katyal, p. 5).Remember from the Explanation section that 1⁄φ = 0.618, and when r = 0.618 it creates a perfect spiral going clockwise and a perfect spiral going counterclockwise. We also get a similar seed distribution that is mirrored at 1 − 0.618 = 0.382. Consider the true relationship of 1⁄φ = φ – 1. If we divide both sides by φ, then we get 1⁄φ2 = 1 − 1⁄φ. So 1⁄φ2 = 1 − 0.618 = 0.382.
There are many other flowers besides the sunflower that are linked to the Fibonacci sequence. Flowers can have a wide range of petals, yet many flowers will typically have 3, 5, 8, 13, 21, 34, 55, or 89 petals. These number of petals correspond to the values in the Fibonacci sequence. Similar to the spacing of seeds, it is believed that flower petals are arranged to maximize the amount of sunlight each petal receives (Ilić, p. 126). Trees also grow according to the Fibonacci sequence, where it starts with one branch, the second year it has two branches, the third year it has three, the fourth year it has five branches, and so on (Katyal, p. 4).

Figure 8: Flowers with Fibonacci-Number of Petals
The golden ratio is aesthetically pleasing, and its beauty has been recognized throughout centuries. We have found the golden ratio in ancient architecture like the Parthenon in Athens (Scott, p. 4). The Parthenon was built using the golden rectangle, where the width is 1 and the length is 1.618 (Ilić, p. 126). One example of the golden rectangle is in the visible spaces between the columns. Watch the video clip below (2:08 - 2:55) to see other golden rectangles in the Greek Parthenon. The Taj Mahal in India is another example of architecture where the golden rectangle is used to create the base structure (Katyal, p. 7).
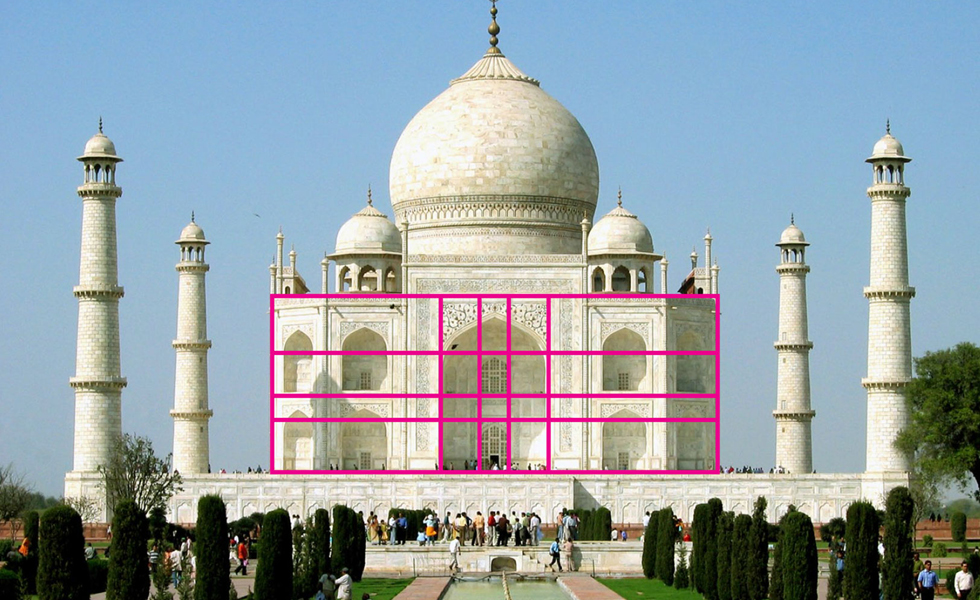
Figure 9: Taj Mahal

Figure 10: Mona Lisa
Similar to the architects of the Parthenon and the Taj Mahal, other artists also utilized the golden ratio to create pleasing proportions in their artwork. Leonardo da Vinci is widely known for his painting of the “Mona Lisa”. Within this painting, we find numerous golden rectangles around her face making her facial features the focal point (Katyal, p. 8). Other works by Leonardo da Vinci also include the golden ratio such as “The Last Supper” and the “Vitruvian Man” (Katyal, p. 7). Knowing that the human body has many golden ratios, we can apply the golden rectangle to the human body and the “Vitruvian Man”.