History of Logarithms
Logarithms are often taught as the inverse of exponents. While this relationship is true, it downplays the significant role the discovery of logarithms played in the evolution of mankind. Surprisingly, logarithms were invented well before exponential notation (Panagiotou, 2010). The major motivation for the discovery of logarithms was a means to simplify multiplication.To understand how revolutionary logarithms really were, we must take ourselves back to a time before calculators existed. Even though calculators did not exist, real-life problems did. Consider Tycho Brahe, for example. He was an astronomer in the late 1500s who set out to disprove the Copernican theory that planets revolve around the sun (Pierce, 1977). To us, this may seem like a trivial pursuit since we have a solid understanding of our solar system, but back then planetary motion was a matter of religious zeal and caused major contention and controversy. In order to come to any sort of conclusion, Brahe needed to make quick and accurate calculations including the multiplication of large numbers.
His problem was that such a means did not exist. Some, including German mathematician Michael Stifel (1486-1567) and French mathematician Nicolas Chuquet (1440-1488), theorized there was a connection between multiplication and addition. Fortunately for us and Brahe, Stifel and Chuquet discovered such a connection (Panagiotou, 2010).
The relationship they discovered can be seen by looking at an arithmetic and geometric progression side-by-side as shown in the following table.
| Arithmetic Progression \((n)\) | Geometric Progression \((2^n)\) |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
Now, consider the following equations:
\(4+7=11\)
\(16*128=2048\)
Referring to side-by-side table, what is the relationship between these two
equations? We can see that the first term in each equation corresponds to
the same row in the table (\(4\) and \(16\)). This relationship holds for the second
and third terms. Amazingly, we have just shown that multiplication can be
simplified down to addition! To find the product of two numbers, we simply
need a side-by-side table that contains the two numbers of interest. Or in
the words of Stifel, "Addition in arithmetical progression corresponds to
multiplication in geometrical progression" (Panagiotou, 2010).\(16*128=2048\)
If our numbers being multiplied were always multiples of two or relatively small, then we would need nothing else. But Brahe was working with outer space! He needed to multiply numbers much larger than 16 and 128 to make astronomical calculations. Additionally, he needed more flexibility in the numbers he used. For example, what if he needed the product of 1003 and 6254? These numbers are not powers of two. In mathematical terms, Brahe needed a table that was more "dense" (Pierce, 1977).
The solution to this problem is credited to English mathematician John Napier (1550-1617). His method started with a line \(TS\), as seeen in the figure below, where the distance between the two points is \(10^7\). Now consider a point \(P\) that starts at \(T\) and moves towards point \(S\). At time \(t = 1\), point \(P\) moves \((1-1/10^7 ) = 0.9999999\) of the distance between \(P\) and \(S\). Point \(P\) is now \(9,999,999\) from point \(S\). At time \(t = 2\), point \(P\) again moves \(0.9999999\) times the distance between \(P\) and \(S\). This pattern is repeated until the distance between \(P\) and \(S\) is infinitesimally small (Pierce, 1977).
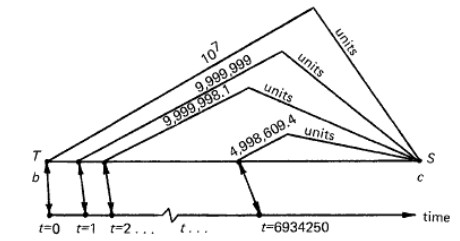
Napier's method for creating a dense table (Pierce, 1977)
Using Napier's method, we can create a side-by-side table as we did before.
| Arithmetic Progression \((t)\) | Geometric Progression \(10^7(1-10^{-7})^t\) |
| 0 | 10,000,000 |
| 1 | 9,999,999 |
| 2 | 9,999,998.1 |
| 3 | 9,999,997.1 |
If we were to continue this progression, it is clear that the right side of this table is denser than the table provided earlier. This table would have a natural number associated to almost every integer between zero and \(10^7\). We could then use this table to accurately compute the product of two numbers using addition.
Napier constructed such a table, which is known as the "Table of Radicals" (Pierce, 1977). He did not calculate every iteration of this table but used ingenious methods of mathematics to simplify the number of repeated calculations (Panagiotou, 2010).
The term "logarithm" entered the scene when Napier introduced a second line. Consider the line \(AB\) where \(Q\) moves at a constant speed of \(10^7\) from \(A\) to \(B\). At some time \(t\), let's say point \(P\) (from the first line) is a distance \(x\) from \(S\) and point \(Q\) is a distance \(y\) from \(B\). Napier defines the segment \(y\) to be the logarithm of \(x\). We can write his logarithms as \(y=Nlogx\), where \(Nlog\) is an object different than the logarithms we use today. Napier realized his system was limited because the \(Nlog1 \not = 0\), which leads to the inconvenient logarithmic property of \(Nlog(AB)=NlogA+NlogB-Nlog1\) (Panagiotou, 2010).
After Napier's death, English mathematician Henry Briggs (1561-1631), upon suggestion from Napier, modified Napier's logarithms to include the idea of a base. Briggs changed Napier's logarithms to base ten so that \(log1=0\) and \(log10=1\), which resolved the inconvenient property (Pierce, 1977). This made logarithms convenient and practical.
The breakthroughs regarding logarithms were quickly and widely accepted. "Indeed, it has been postulated that logarithms literally lengthened the life spans of astronomers, who had formerly been sorely bent and often broken early by the masses of calculations their art required" (Pierce, 1977).
Later, Swiss mathematician Leonard Euler (1707-1783) in his book Complete Introduction to Algebra devised our current notation that officially connected logarithms to exponents. (Pierce, 1977).
"If \(x>0\), the logarithm of \(x\) to base \(a\) \((a>0, a =/1)\), is the
real number \(y\) such that \(a^y=x\) and is symbolized with \(y=log_ax\)."
--Euler (pp. 63-64 of Complete Introduction to Algebra)
As stated at the beginning of this page, the discovery of logarithms as the
connection between multiplication and addition that had long been theorized
was a necessary mathematical breakthrough that moved society forward
(See Applications).