The mathematics behind breaking the Vigenère cipher are actually very simple. Charles Babbage noticed that in a messaged enciphered with the Vigenère cipher there would be repeated groups of letters. He figured that was either happening because the same word got enciphered with the same part of the key, or it just happened by chance. In order to ensure that it was from former rather than the latter he looked at repeated segments that were longer. By counting the number of letters in between repeated segments he could guess the length of the key word or phrase. For example, if there were 15 letters in between the repeated segments the key phrase could be 15 letters long, meaning it cycled through once before starting again, 5 letters long and it cycled through 3 times before the same word was written agian, or 3 letters or 1 letter long. Obviously the key word wouldn't be one letter long because then you would have a monoalphabetic cipher and that could be broken with frequency analysis. This process of finding repeated segments was repeated until the length of the keyword was decided on (Singh 2016).
The key to breaking the cipher is finding the greatest common factors of the lengths of intervals between repeated segments. It can be useful to create a table to sort out the factors and see which ones are repeated.
| Spacing | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 30 | X | X | X | X | X | ||||||||||||||
| 20 | X | X | X | X | X | ||||||||||||||
| 120 | X | X | X | X | X | X | X | X | X | X | X |
Only the factors that are common for all the spacings are possible lengths of the key. We can see that the possible keys here would be a length of 2, 5 or 10. If there were no more repeated segments we could then look at the frequency analyis of each possible alphabet. For example, with a key length of 2 every other letter would be part of the same alphabet. You can run frequency analysis on that and see if the graph matches the general shape of the expected shape.
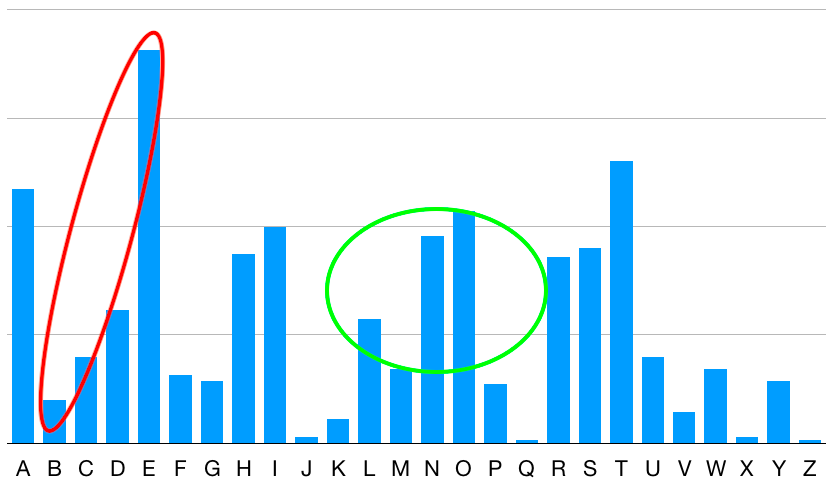
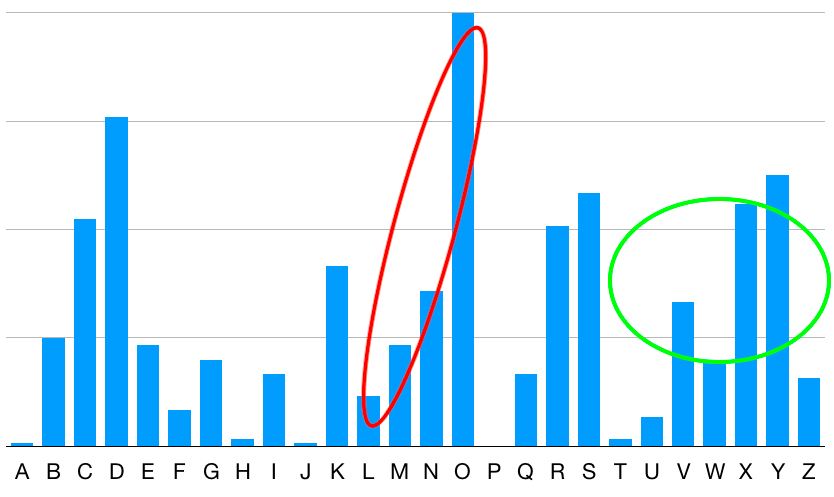
Here is a hypothetical example of what the freqency chart would look like for a spacing of 10. Notice how the peaks are similar, but are in different places. We could conclude by looking at this that the keyword is likely 10 letters long, and that at least for this particular alphabet, O is very likely to be E. The process would be repeated for as many alphabets were needed to be able to pick out a message.
The longer the keyword, the more difficult the Vigenère cipher is to break because it splits the message into more alphabets making the number of letters smaller. This makes frequency analysis difficult, but not impossible. An unbreakable form of cryptography is found by using a one time pad. If the length of the keyword is exactly equal to the length of the message then each alphabet used to encipher the plaintext has only one letter in it. This means that it would be impossible to use frequency analysis on each individual alphabet. In addition to that, every possible combination of letters is a possible outcome. If n is the number of letters in the key, then there are n to the 26 possible keys. This means that even if you had the time to somehow use brute force, you could certainly come up with the right decryption, but you will also come up with many messages that make sense, but are not the correct decryption. If "NAIFHEPWMASOFBT" was the cipher text, both "meet me at the park" and "I need a new target" could be the possible decryption because they have the same number of letters. The keywords for both of the are different, but without knowledge of the keyword we don't know what the actual message is supposed to say. The one time pad is the only method of encryption that is proven to be impervious to attacks. Some are impossible to break without brute force, but even the one time pad could not be broken with brute force.
Below is an applet created by me that explains how the Diffie-Hellman key exchange works. The process is relatively simple. For this applet to work properly, use values that are below 20. In all reality, the values used in the Diffie-Hellman key exchange should be large, each number being around $2^{1000}$. This makes the brute force method of trying every possible key is too time consuming to be effective.
Here we will prove that the RSA algorithm works. This proof is adapted from the proof by Barry Steyn on this website.
The key to why RSA cryptography works is Fermat's Little Theorem which states: $$a^p\equiv{a}\text{ mod }p$$ Fermat's Little Theorem can be rearranged by dividing both sides by a to get $$a^{p-1}\equiv{1}\text{ mod }p$$ Before we start working with the encryption and decryption we have to set some things us. First we need to choose two prime numbers p and q. These should be randomly cohosen and should be large and far apart. The modulus, n, of our encryption and decryption functions will be the product of p and q.This is the key to the security behind RSA cryptography. It is easy and fast for a computer to multiply two numbers together, but reversing the process and factoring a number is time consuming and very difficult.
Next we need to compute the totient of n, which is the number of numbers less than n that are relatively prime to n. The totient of a prime number, p is p-1, by definition of a prime number. The totient of the producto of two primes is the product of their respective totients, so, $$\phi(n)=\phi(p\cdot{q})=(p-1)(q-1)$$ Finaly we need to make a public and private exponent. The public exponent for any RSA algorithm is usually 65537 because it is faster to use a smaller number. It doesn't matter what the public exponent is as long as it is prime. We will call our public key d. The private exponent, which we will call e, is the multiplicative inverse of d modulo the totient of n. This can be found using the extended Euclidean algorithm. When multiplicative inverses are multiplied together, they equal 1. $$e\cdot{d}\equiv{1}\text{ mod }\phi(n)$$
Now it is time for our encrypting and decrypting equations. m is plain text and c is cipher text. $$E(e,m)=m^e\text{ mod }n=c$$ $$D(d,c)=c^d\text{ mod }n=m$$ Let's prove that this works.
Since $c=m^e\text{ mod }n$ we need to prove that $$D(d,m^e)=m$$ or in other words, that by putting our encrypted message into our decrypting formula, that we'll get out the plain text message. We will start with what we know. $$D(d,m^e)=m^{ed}\text{ mod }n$$ Because e and d are multiplicative inverses of each other in $\text{mod }\phi(n)$ then $$ed=\phi(n)\cdot{k}+1$$ for any integer k, so $$m^{ed}\text{ mod }n = m^{k\phi(n)+1}\text{ mod }n$$ Now we know that $\phi(n)=(p-1)(q-1)$ so we can say $$m^{k\phi(n)+1}\text{ mod }n = m^{k(p-1)(q-1)+1}\text{ mod }n$$ This next part we will be focusing on p, but it is true for q as well. $$m^{k(p-1)(q-1)+1}\text{ mod }n=(m^{p-1})^{(q-1)k}m\text{ mod }n$$ Now we an apply Fermat's Little Theorem. Since p is prime, $$m^{p-1}\equiv{1}\text{ mod }p$$ This means that $$(m^{p-1})^{(q-1)k}m\text{ mod }n=({1}\text{ mod }p)^{(q-1)k}m\text{ mod }n$$ And since p divides n we can say $$({1}\text{ mod }p)^{(q-1)k}m\text{ mod }n=1\cdot{m}\text{ mod }p$$ Remember what we started with? $$m^{ed}\text{ mod }n=m\text{ mod }p$$ This is also true for q, so $$m^{ed}\text{ mod }n=m\text{ mod }q$$ Because p and q are both prime and p times q is n then $$m^{ed}\text{ mod }n=m\text{ mod }pq$$ $$=m\text{ mod }n$$ The RSA algorithm works both ways, meaning you can encrypt with either function and the opposite will decrypt.
Both the Diffie-Hellman key exchange and RSA rely on what are called one way functions or trap door functions. These are easy to do, but hard to undo. One example of a trapdoor function that is taken advantage of in the RSA system is multiplying primes. How long does it take you to find the factors of 629? What process did you use to find them? A computer has a few algorithms that optimize the time it takes to find factors, but it still is essentially trying one prime number after another until a remainder of zero is found. In cryptography numbers larger than 17 and 39 are used. The standard for encryption right now is 2048 bit encryption, which is numbers that are 617 digits long. If you were trying to factor that with a standard desktop computer it would take 6.4 quadrillion years (Digicert).