As long as humans have been alive, they have had secrets and they have developed ways to hide those secrets. Beginning with stenography, the art of hiding messages, and then moving to cryptography, the art of writing in codes, this field is continually evolving. In this webpage we will go through a brief history of cryptography, beginning with Caesar and ending with quantum computing.

One of the first ciphers used was the Caesar Cipher. Julius Caesar aparently sent all of his messages with an alphabetacal shift of 3. This meant that A became D, B became E and so on. This cipher wasn't very secure because there are only 25 different shifts, so one only needs to try 25 different codes to find the right one.

To make up for the lack of security of the Caesar Cipher, people started using any letter to replace any other letter in the alphabet. This meant that A could be any of the 26 letters of the alphabet, B could be any of the 25 remaining letters, C had 24 options and so on. In all there are 26! different ways that one rearrange the alphabet which meant the brute force method of trying every option was out of the question. The substitution cipher was secure for the time being.

Monks interested in finding the secrets of the Koran began keeping track of how many times each letter was used. They established the overall frequencies of letters. This information was not used for breaking codes until it was realized that whichever letter or symbol was used most frequently in the cipher text would likely be the letter that was used most often in whatever language the plaintext was written in. By analyzing texts in different languages, frequencies tables of letters were created. Once they guessed a few of the common letters, codebreakers were able to find entire words and then break the code. The security of the substitution cipher was lost (Singh, 2016).

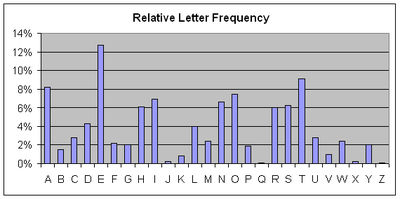
Frequency analysis is not perfect. The shorter the text, the less likely the letters are to show up in the expected frequencies. In fact, two books have been written without using the letter E. The first one was in 1939 written by Ernest Vincent Wright. It then inspired a French author named Georges Perec to write a novel without using E as well. Arguably more impressive, Perec's book has been translated into English, German, Italian, Dutch, Swedish, Spanish, Romanian and other languages, also avoiding the letter e. Frequency analysis can also be made more difficult. People began using nulls, or symbols that didn't represent any letter. Codemakers also created multiple symbols to represent common letters in order to lower their frequency and make their true value less obvious. These could be broken by looking at digraph and trigraph frequency, or the frequencies of groups of letters rather than individuals.

One of the most famous cases of a cipher was the case of Mary Queen of Scots. Mary was imprisoned by her cousin Elizabeth because of her threat to the throne. Elizabeth was Protestant and Mary was Catholic. Mary's Catholic supporters wanted a Catholic on the throne to ease their persecution. One of these supporters, Anthony Babington, had been planning an assasination of Queen Elizabeth, but they wanted Mary's blessing. He contacted her with an enciphered message explaining the plot. The enciphered message had nulls and characters representing different letters. He believed that the cipher was unbreakable. Unfortunately, unbeknonst to both Mary and Anthony their letters were being intercepted and decrypted. Once they had enough evidence they were able to bring them in and convict them. Mary and the rest of the conspirators were sentanced to death (Singh, 2016).

The next big step in cryptography came with the development of polyalphabetic ciphers. Everthing used up to this point was a monoalphabetic cipher meaning each letter could only be represented by one or more symbols or letters and those symbols and letters could only map back to one letter. In 1404 an Italian man named Leon Battista Alberti thought of the concept of encrypting a message by alternating between two ciphers. This gave the advantage that a single letter in cipher text could represent two different plaintext letters. This idea was advanced and developed further by several men until Blaise de Vigenère created the Vigenère cipher.

The Vigenère cipher is powerful because it has 26 possible alphabets. By establishing keyword, sender and receiver can agree on how to switch between alphabets. The chart shown above is universal for anyone using the Vigenère cipher. Let's work through an example to explain how to use this cipher.

Suppose we wanted to send the word "Cryptography" and we had previously decided on the key word "dogs." We start by writing DOGS repeatedly over our plaintext.

D O G S D O G S D O G S
C R Y P T O G R A P H Y

The letter that is above the plaintext is the cipher alphabet we are going to use to encipher that letter. The alphabets that we are going to use in our example are shown below. The plain text is highlighted red and the cipher alphabets are highlighted in yellow.

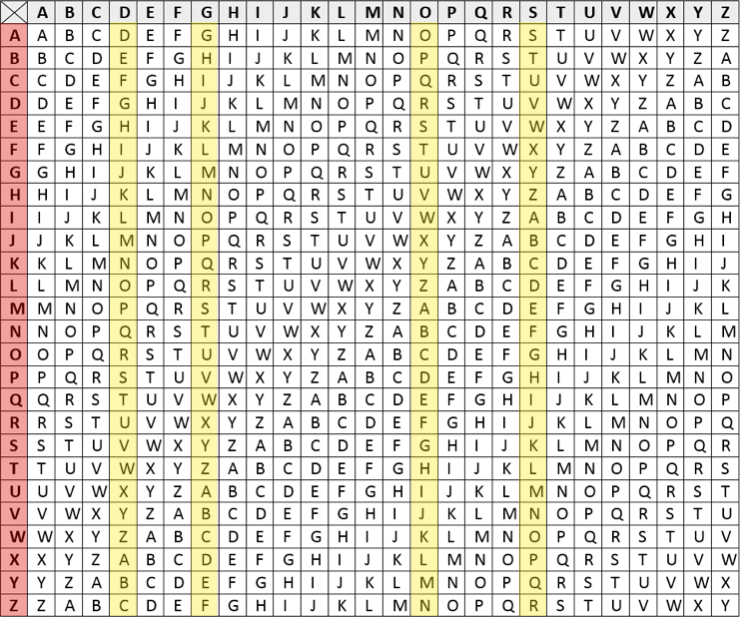
To encipher the letter C we will use the alphabet in the D column. In that column we go down to the row with C in the plaintext alphabet. Where the D column and the C row intersect is F, so C is encyphered as F. The next enciphered letter is F because that is where O and R intersect. Here we can see the main advantage of the Vigenère cipher because two different letters can be enciphered as the same letter. In the same manner, the same letter can be enciphered as different letters. This makes frequency analysis an ineffective strategy. Our final encrypted message would be FFEHWCMJDDNQ. Decrypting the message is the same process. You start by writing the word "dogs" repeatedly over the cipher text.

D O G S D O G S D O G S
F F E H W C M J D D N Q

Then one by one you use the alphabets indicated to decrypt the message, this time finding the letter in the appropriate column and writing down which row it is in.

The Vigenère cipher was thought to be unbreakable for many years, then Charles Babbage, the man who made plans for the first computer, cracked the code just to prove a point to a friend. The weakness of the Vigenère cipher was its cyclical nature. He found that if he could find a repeated group of letters in a text it was likely because the same word lined up with the same letters from the keyword, thus having them be enciphered the same way. He found that if he could find the length of the keyword, he would be able to apply frequency analysis to each individual alphabet. A deeper explanation of how to break the Vigenère cipher is found here

Although Charles Babbage broke the Vigenère cipher, he had to keep it secret because it was still the main cipher used by militaries throughout the world. The British government wanted other governments to believe that their communication was still secure. This was the case for many cipher breakers throughout history. Because of the nature of what they are doing, successes are often kept secret until they are no longer needed.

One of the most famous types of enciphering that came after the era of the Vigenère cipher was the Enigma machine. The Enigma machine and other similar enciphering machines were polyalphabetic ciphers, but relied on mechanics to avoid cycling through the same alphabets. Since there are many movies, books and websites dedicated to the Enigma and those that broke the code, I won't spend much time here talking about it. One of my favorite sources is here because it tells the often untold story of the Polish codebreakers that initially broke the Enigma cipher.

The invention of computers allowed for more and more complicated algorithms to encipher messages. These algorithms relied on a shared keyword to encipher and decipher the message. As computing moved forward, people saw a need for privacy for the common person, not just for militaries and governments. One of the main problems that needed to be solved was that of key distribution. If I wanted to send my friend a message I would first have to meet with them or send a trusted person to exchange the key with them. Only then could I communicate securely. If I wanted to talk with several people that were in very different places, this would become difficult and costly. Governments, militaries and big businesses could afford this, but the commmon man couldn't. Many people tried to solve the problem of key exchange. One of them was named Whitfield Diffie. He got connected with two other people named Martin Hellman and Ralph Merkle who were alo interested in solving the problem. They spent a lot of time trying to figure out how to solve the problem until one night Ralph Merkle had a mathematical revelation. He shared it with Diffie and Hellman and together the men implemented the system. An applet and explanation of the algorithm is found on the math page here.

Another major advancement in cryptography came when Ron Rivest, Adi Shamir and Leonard Adleman came up with an implementation for public key cryptography, which eliminated the need for key exchange. RSA is a form of public key cryptography. Imagine you had a message you wanted to send your friend. In any previous forms of cryptograpy, you would write the message and lock it in a box. Your friend, who has the same key as you, would be able to unlock the box. With public key cryptography you are able to distribute boxes with unlocked padlocks on them to anyone who wants to talk with ou. Anyone is able to send a message to you and lock it up in the box, but only you have the key to the padlock. Even the sender wouldn't be able to unlock or decrypt their own message.

Because of the complexity of the algorithms encrypting the messages, it would take longer than the lifetime of the universe to break the codes with a standard desktop computer. But people aren't trying to decrypt things with a single, standard desktop computer. Advancements in quantum computing are cutting down on the time it takes to decrypt messages using brute force. This has lead to some major advancements in cryptography. One of these advancements is called hashing. Hashing is a way of storing data using an algorithm. Two way hashing converts the data into a unique key. The hashing process can then be reversed using the key to access the data. If the hashtable only goes one way, meaning you can store the data, but you can't reverse the process to access it, it becomes a useful way of storing passwords. For example, when someone creates a new account with a new password, the password gets hashed and is connected with the person who created the account. Then in the future when someone tries to log into the account the password entered is hashed again, then compared to the previously hashed password. If hashed passwords match, the person is allowed into the account. The cool thing about hashing is that not even the programers have access to what the actual password is, only the hashed one. This function is truly one way because once a password is hashed, it can't be unhashed. Someone trying to break in wouldn't be able to guess what the password is based on the hashed version, and the hashed version won't get them into the account (Garner).