Volume of a Cone using Calculus

In his video titled 'Find the Volume of Any Shape Using Calculus', Dominic Walliman thoroughly explains how he proved the volume of a cone using calculus, more specifically using integrals. He started by using cylinders to estimate the volume of a cone, as finding the volume of a cylinder is relatively simple. He sectioned the cone into 4 cylinders and doing so allows him to find the area of those cylinders and add them up to approximate the volume of the cone. (pictured below)

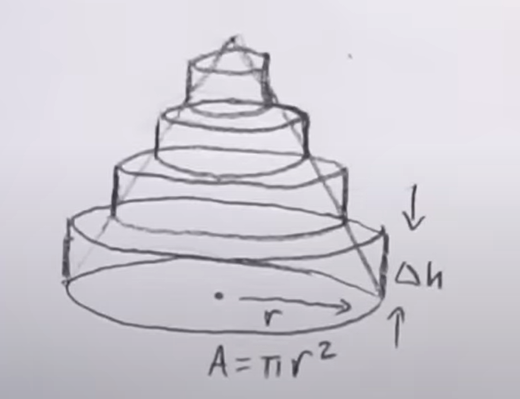
To find the volume of the cylinders we multiply the base (area of the circle) by the height. Williman gave the cylinder's radius a length of 'r' and height of \(\Delta\)h. Then to find the approximate volume of the cone, you add up the volumes of the cylinders, thus getting this equation: V=\(\sum\pi r^2\cdot\Delta h\) approximately. Williman goes on to say that if we make infinitely many cylinders, and have their heights be infinitely small, then the resulting sections of cylinders will take the shape of the cone, allowing us to calculate the exact volume of the cone (this is using Cavalieri's principle). To do so, first Williman then expressed the sum in terms of h. After some algebra, the equation mentioned above becomes: V=\(\sum\pi\frac{R^2}{H^2}\cdot h^2\cdot\Delta h\) (the reader can reference the video to see how this equation was obtained). Since the heights of the cylinders are infinitely small, and there are infinitely many of them, the summation now becomes an integral, thus getting the following equation: V=\(\pi\frac{R^2}{H^2}\int_0^H h^2dh\). After completing the integration, the reader is left with the formula for the volume of a cone which is V=\(\frac{1}{3}\pi r^2\cdot h\). Thus the reader can see how one can use calculus to derive the formula. At the conclusion of his video, Williman explained that using similar methods one can derive the volume for many other shapes.

Volume of a Sphere Using Calculus

Similarily, the equation for the volume of a sphere can also be derived using calculus. In a video posted by Instanze titled, 'Volume of a Sphere' this concept is explained more fully. He starts by explaining that spheres are radially symmetric. With this in mind, he starts by taking a semicircle with radius 'r' and places it along a central axis, and then he revolves the semicircle 360 degrees about the central axis creating a sphere with radius 'r'. He then uses the 'disk method' on one of the cross sections to proceed (pictured below).

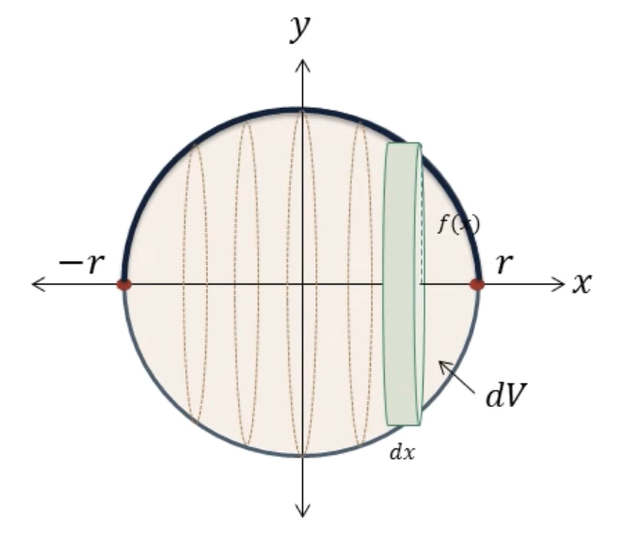
Taking one of the disks, he centers it at the origin with the diameter from '-r' to 'r'. Thus the equation for this disk is \(x^2+y^2=r^2\). Instanze proceeds to solve for 'y', and since we are just looking at the positive side, he drops the plus or minus sign getting: \(f(x)=\sqrt{r^2-x^2}\). From the 'disk method' for a sphere, we know the volume is equal to \(\int_{-r}^r dV=\int_{-r}^r \pi [f(x)]^2dx\). Then after plugging in the equation we found for \(f(x)\), the radical and the square cancel out leaving \(\pi\int_{-r}^r (r^2-x^2)dx\). Then after the integration, you are left with the formula for volume of a sphere which is \(V=\frac{4}{3}\pi r^3\)

Connections Between Volume and Surface Area Using Calculus

In addition to deriving the formulas, one can also use calculus to find connections between surface area and volume. From the previous paragraph, the reader saw how the formula for the volume of the sphere was derived giving us \(V=\frac{4}{3}\pi r^3\). The formula for the surface area of a sphere is \(SA=4\pi r^2\). It is interesting to note that the derivative of the volume formula gives us the surface area formula. Similarly, the circumference of a circle is the derivative of the area formula for a circle. In his video titled “A Volume/Surface Area Query in Calculus (Tanton Mathematics), Dr. James Tanton explains this connection further, specifically the connection between the formula for the volume of a sphere and the formula for the surface area of a sphere. Tanton starts by looking at the definition of a derivative in the terms of a sphere with radius 'r' and a sphere with radius 'r+h'. (pictured below).

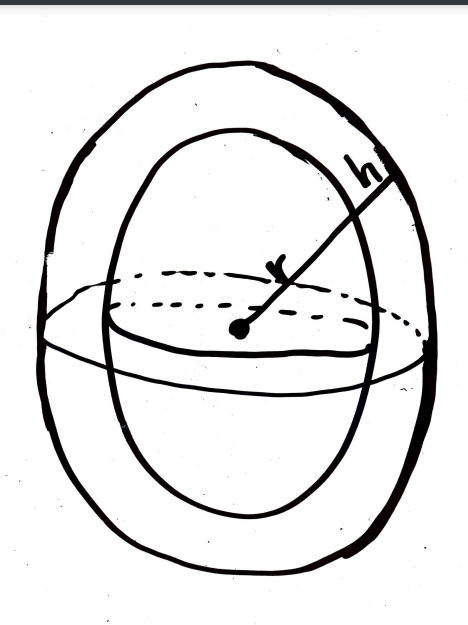
Thus he gets: \(\frac{dV}{dr}=\lim_{h\to 0} \frac{V(r+h)-V(r)}{h}\). After taking the difference of those two volumes, you are left with this shell that is 'h' thick. Therefore we get that \(V(r+h)-V(r)=SA\cdot h\). After subtracting the smaller sphere, we are left with the surface area of the bigger sphere, but that shell that was mentioned before is thre too, thus we have to multiply the surface area by \(h\). If plugged back into the definition of a derivative the equation becomes: \(\frac{SA\cdot h}{h}=SA\). Thus calculus can be used to show interesting relationships between area and volume.