According to The American Mathematical Society (2002) Morrin showed an interest in mathematics and philosophy. Morins' father believed that since his son was blind he would not do well in mathematics so he encouraged him to pursue philosophy (American Mathematical Society, 2002, 1247). "After studying at the Ecole Normale Superieure for a few years, Morin became disillusioned with philosophy and switched to mathematics (American Mathematical Society, 2002, 1248)." The American Mathematical Society (2002) states that before Morin ever finished his Ph.D. he was already well known for his work in sphere eversion. Mathematicians who have worked on the problem of everting a sphere "overwhelmingly noted that their main motivation was a desire to see a sphere eversion (STEINGART, 2015, 46)." In 1957 Smale surprised the mathematical community when he published a paper in the Transactions of the American Mathematical Society formally proving that a sphere could be turned inside out following the rules of topology (STEINGART, 2015, 51)." What this proof did not show was how do to it. This video explains the rules and demonstrates how a sphere is everted.

In an interview about sphere eversion Morin said "our spatial imagination is framed by manipulating objects . . . you act on objects with your hands, not with your eyes. So being outside or inside is something that is really connected with your actions on objects (STEINGART, 2015, 56)." Morrin is well known for his work in sphere eversion and used clay models to show how to every a square. Try grabbing some clay or playdough and lets do the same. To be able to do this you must know the rules. 1. The sphere can pass through itself (the top can push through the bottom) 2. You can not puncture or cut the sphere 3. You can not get any creases or sharp corners This video animates the steps that we will be molding. Watch this video until 4:33

Try play around for a little bit before following the step below. Mold the following figure

Now you need to mold this. The top and the bottom should look exaxtly the same

This is the next step the blue is the bottom passing throuhg the top.

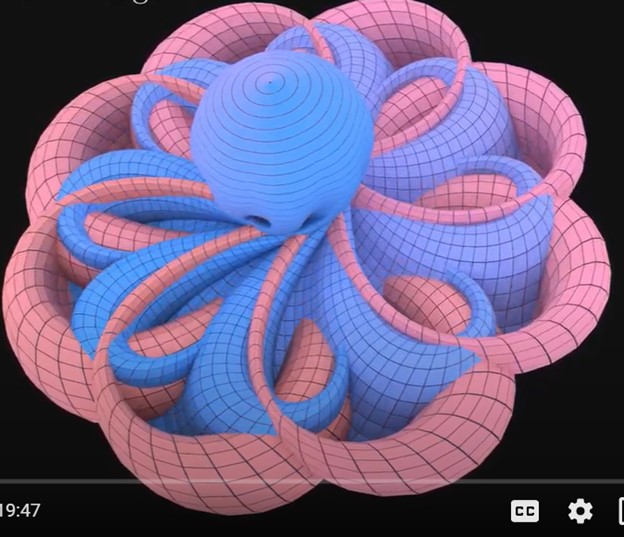
The bottom has mostly passed throught the top and this is what we are left with.

Now you are elongating the figure to try and straighten everything out.

Now we are flipped inside out and return to something that looks like the first step.

Lastly we end up with an everted sphere.