◰ Introduction

Have you ever wondered how we now so much about space? We haven't been able to get into space for very long as a species. But we know locations for stars as well as distances to other celestial objects. We also know how big these objects are. Find out more by clicking the buttons below.

There are several ways to measure mass in space. Applications of the different methods depends on the size of the object that you want to measure. The objects that we are going to focus on are celestial objects. Things like planets, stars, comets, or asteriods.

◰ History of Mass of Celestial Objects

Weight can't be measured in space because weight depends on the gravitational pull of things around you. Instead, objects in space are distinguished by their mass. Mass is a measure of how much matter something contains. There are several ways to find and estimate mass depending on the type of object that we are talking about. Let's just focus on the mass of large objects such as stars, planets, asteriods, and galaxies.

Isaac Newton was concerned about finding the mass of large objects. He described the first mathematical representation of the relationship between distance, mass, and force of gravity. Then, he proved it by showing that the path of a comet follows a parabola in 1680 before publishing his work in 1687. Calculating something as big as the mass of the Earth or the Sun also requires the idea of Einstein's called special relativity, published in 1905. This theory treats time, space, and mass as fluid things that depend on your frame of reference. However, at large scales, the differences in time, length, and mass predicted by relativity are small enough that they appear to be constant which allows us to continue to use Newton’s law of universal gravitation.

Henry Cavendish was the one to solve for the "universal gravitational constant. He was also the first person to attempt to calculate the mass of the Earth from his experiments finding the universal gravitational constant in 1798.

But what exactly is going on? Here's a short video on Newton's Law of Universal Gravitation and how it was used to solve for the mass of the Earth (or any object).

Mass Podcast Transcript

◰ Math of Celestial Objects' Mass

First we need to find a mass so that we can compare it to everything else. This is why we find the mass of the Earth. Since the podcast describes a way to do so by comparing the earth to itself we will show the algebra involved. Let m_E be the mass of the Earth, a be the acceleration, r be the radius of the Earth, and G be the gravitational constant. We can set \(F_g = m_1 \cdot a\) and \(F_g = G \cdot \frac{m_1 \cdot m_2}{r^2}\) equal to each other because they are both measuring force. Note that we are comparing earth to itself so $$ m_E = m_1 = m_2$$ Then the equation that we currently have is $$ m_E \cdot a \frac{m}{s^2} = G \frac{N \cdot m^2}{kg^2} \cdot \frac{m_E^2}{r^2 m^2}$$ Now we can put in all the values that we know. $$m_E \cdot 9.8 \frac{m}{s^2} = 6.647 \cdot 10^{-11} \frac{N \cdot m^2}{kg^2} \cdot \frac{m_E^2}{(6.371 \cdot 10^6)^2 m^2}$$ We also know that \(1N = 1\frac{kg \cdot m}{s^2}\) so we can also substitute that in. $$m_E \cdot 9.8 \frac{m}{s^2} = 6.647 \cdot 10^{-11} \frac{kg \cdot m^3}{s^2 \cdot kg^2} \cdot \frac{m_E^2}{(6.371 \cdot 10^6)^2 m^2}$$ Now we simplify $$m_E \cdot 9.8 = \frac{(6.647 \cdot 10^{-11})(m_E^2)} {(6.371 \cdot 10^6)^2 \text{ kg}}$$ And divide by \(m_E\) on both sides to find that $$9.8 = \frac{(6.647 \cdot 10^{-11})(m_E)} {(6.371 \cdot 10^6)^2 \text{ kg}}$$ Then, we are able to multiply by the reciprocal to solve the equation for \(m_E\) as follows: $$m_E = \frac{(6.371 \cdot 10^6)^2)(9.8)} {(6.647 \cdot 10^{-11})}\text{ kg}$$ $$m_E \approx 5.96 \cdot 10^24 \text{ kg}$$ Now that we have found the mass of the Earth, we can use Newton's Law of Universal Gravitation to find the masses of other objects by finding the force that they exert on the Earth.

◰ Applications of Mass of Celestial Objects

Why does the mass even matter? Scientists objects to help classify objects. This is how Pluto became classified as a dwarf planet in August of 2006 by the International Astronomical Union. To learn more about this debate watch this video.

For scientists to apply this to objects other than the Earth, they need to find the acceleration of thee other objects. You can find the acceleration by measuring how fast objects go around each other (stars) or you can find it by finding how fast the object rotates (galaxies).

Scientist also used this method to find the mass of other planets in other galaxies. Especially in their search for an Earth-like world that could hold life such as our. You can read this article from Science News for Students for more about this

There are a lot of ways to measure distance in the universe and they all build on each other. To capture all the different ways that astronomers use to measure distance in the universe, they have created a metaphor of sorts. It is called the "cosmic distance ladder" because all of the rungs require the technique(s) before it to be able to use that technique accurately.

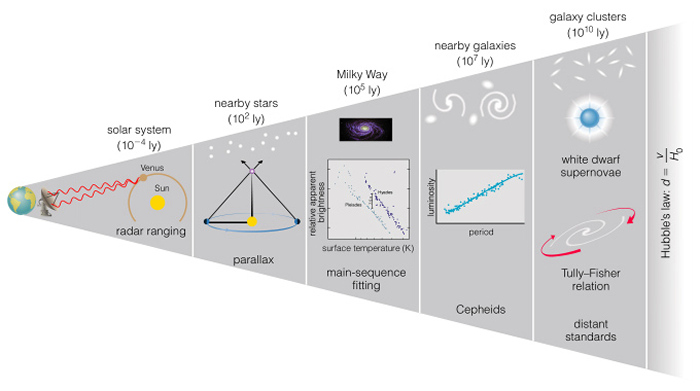
Let's get a quick overview of the different ways to measure distance in space.

We are going to focus on 3; stellar parallax, radar ranging, and the distance modulus or spectroscopic parallax.

◰ Parallax

What is the parallax? It is easier to show you what this is than to explain it.

▣ History of the parallax

Stellar parallax is the oldest way that we have of measuring the distance to stars. Aristarchus, an ancient Greek astronomer (310-230BC), measured the angular separation (the angle between where the center of the moon appeared and the center of the sun appeared) between the Sun and Moon when the moon was half-full which allowed him to derive the distance between the Earth and Moon in terms of the distance between the Earth and the Moon (with some trigonometry). His idea was correct, but his measurements were not. He thought the Sun was 19 times farther from Earth than the Moon, in reality it is approximately 390 times farther. This was also the first time that it was assumed that the Earth orbited around the sun.

Nicolaus Copernicus (1473-1543 AD) was able to determine approximate distance to other planets through trigonometry with this method, but these were all found to be relative to the distance between the Earth and the Sun. This meant we needed an accurate measurement of that distance.

Eratosthenes (276-194BC) estimated the Earth to Sun distance. There is some disagreement in which value is the correct translation, but if you consider the one that is the most accurate, Eratosthenes estimated that the distance is between 126 million and 168 million kilometers, which includes the actual Earth-Sun distance of about 150 million kilometers. Which is fairly accurate, but because of translation issues, we aren't sure if this is true or not.

The first rigorous and accurate scientific measurement of the Earth-Sun distance was made by Giovanni Cassini in 1672 by parallax measurements of Mars. He and another astronomer observed Mars from two places simultaneously. Then they used trigonometry to calculate the parallax. His calculations put the measurement at 140 million kilometers.

There were several other astronomers who attempted to measure this distance accurately. In combination with several other scientists, Jérome Lalande found the first robust estimate of the Earth to Sun distance. Published in 1771, this estimate was 149,597,870.7 km, not far from the modern value.

The distance between the Sun and the Earth in called the "astronomical unit". It was originally defined as the Cassini measurement. However, it was changed to "the radius of an unperturbed circular Newtonian orbit about the Sun of a particle having infinitesimal mass, moving with a mean motion of 0.01720209895 radians per day (known as the Gaussian constant)" because technically the orbit of the Earth is elliptical not circular. Then, on September 19, 2012 the International Astronomical Union voted to change it to a fixed 149,597,870,700 meters, which is the mean distance between the Sun and the Earth.

The stellar parallax of stars other than the Sun didn't was not done (or able to be done) until German astronomer Wilhelm Struve chose to focus on stars that were closer. He reasoned that stars that are closer would have a more noticeable parallax. He was not, the first person to publish this though. Friedrich Bessel was the first to publish a reliable measurement of parallax in 1838.

▣ Math Behind A Parallax

Let's get an example of how to use this method before we use more generic variables to represent what is going on.

Basically, what we are doing is forming an isosceles triangle with the Sun as the midpoint of the base, the length of the base as twice the distance from the Sun to the Earth, the distance from the Sun to the star as the height of the triangle, and the parallax angle as the angle directly above the Sun (like the image below).

This means that we know that $$ \tan{\frac{\rho}{2}} = \frac{AU}{d}$$ and from there we can solve this for the distance, d , as follows. $$ d \cdot \tan{\frac{\rho}{2}} = AU $$ $$ d = \frac{AU}{\tan{\frac{\rho}{2}}}$$

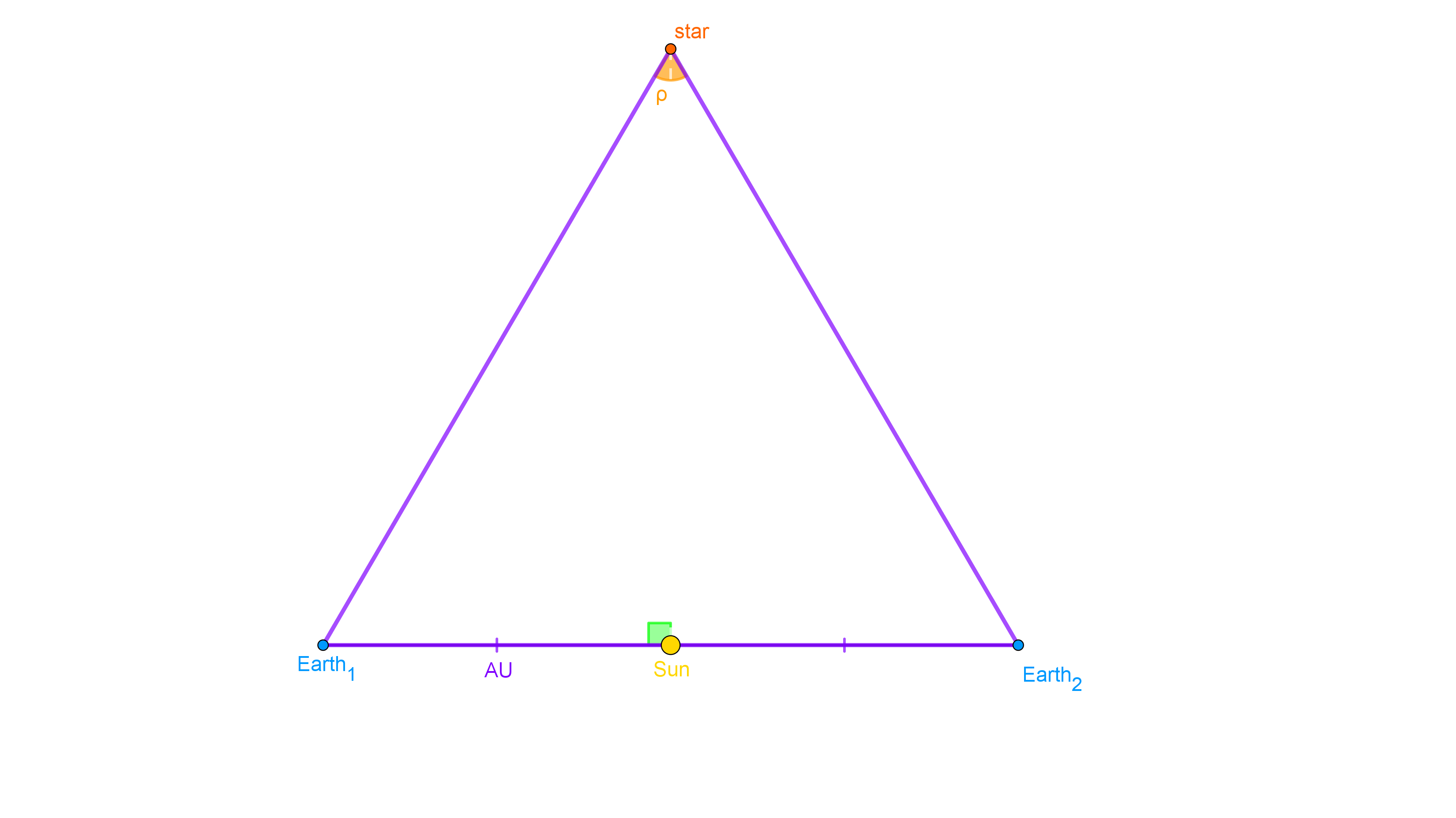
▣ Applications of the Stellar Parallax

Parallax is the oldest idea to date, but it is limited. Because of the atmosphere, from Earth this method is only reliable for a few hundred light-years (about 1.89 x 10¹⁸ kilometers). This is relatively short because the Milky-Way galaxy is 100,000 light years across (10¹⁸ kilometers) across. However, The Hubble telescope is the farthest to date, being able to find the parallax of stars up to 7,500 light years away (7.095 x 10¹⁹ kilometers) as of April, 2014, since it is not limited by the atmosphere of the Earth.

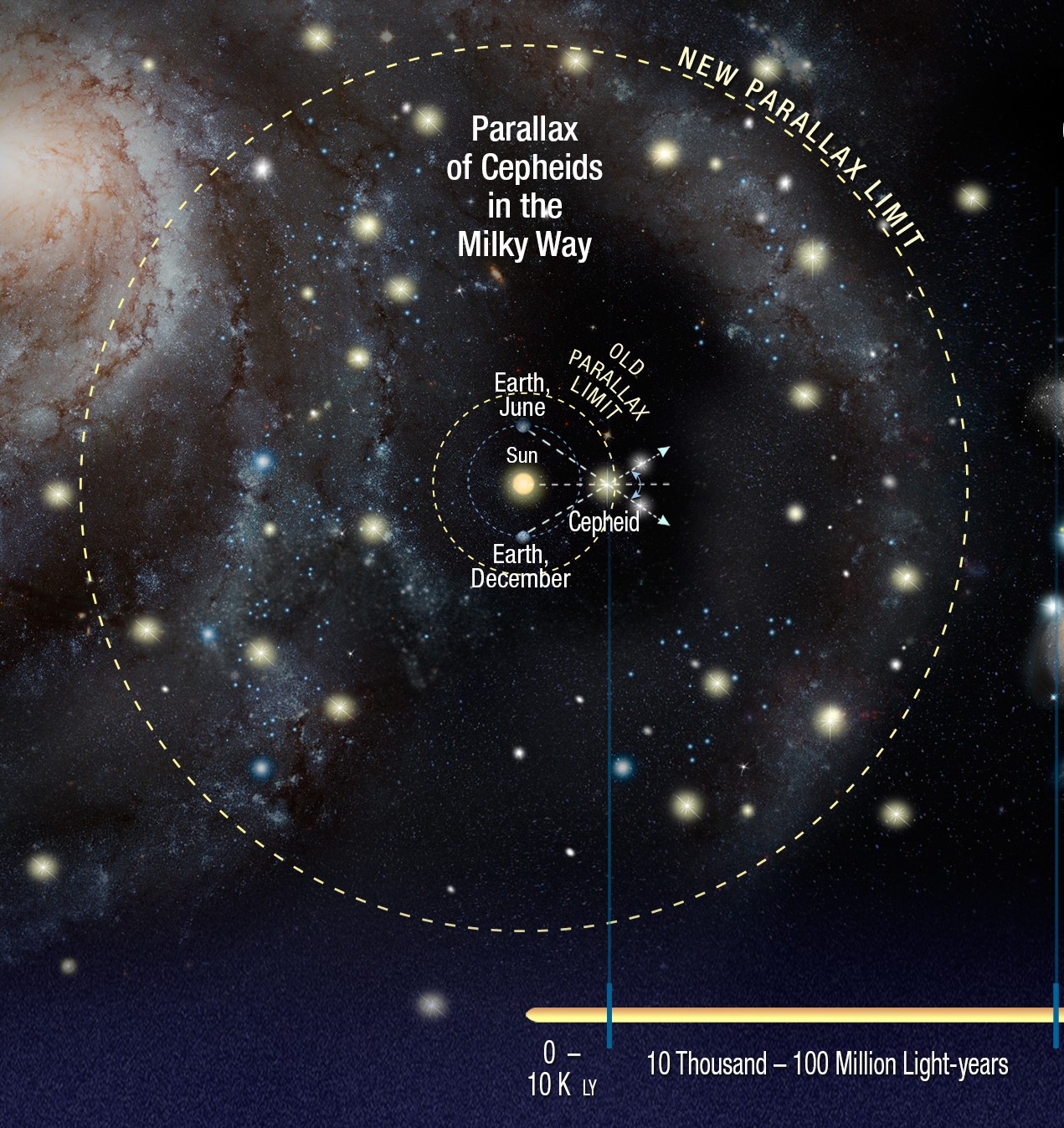
Also, because of advances in space flight and having satellites around every planet in our solar system, measuring the parallax is not the only way to measure distances to planets in our solar system. There are also additional ways to measure distances to objects that are even farther away.

◰ Radar Ranging

Let's start with confidently finding the distance to other planets in our solar system and using that to find the modern value of the distance from the Sun to the Earth. Here's how it works.

▣ History of Radar Ranging

This technique started out as a tool mainly developed as a result of World War II as a way to identify enemy warcraft. The idea was introduced in June of 1922 by Guglielmo Marconi. Later, Sir Robert Watson-Watt used the same idea (bouncing radio energy off of things to calculate the distance) to measure the distance to the ionosphere on January 28, 1935. The first successful attempt to bounce radio waves off of asteroids was in July of 1946 by a group of professional and amateur scientists lead by Sir A. C. Bernard Lovell in Britain at the University of Manchester. The first unambiguous detection of radio waves from farther in our solar system was done by the Jet Propulsion Laboratory on March 10^th, 1961 and they bounced waves off of Venus. The development of radar astronomy was pushed on by the Cold War and the consequent Space Race. After, Mercury was detected by a group of scientists under Vladimir A. Kotelnikov in June 1962. Richard Goldstein made the first radar detection of Mars in February of 1963. Both the U.S. and the Soviet Union attempted to use radar to detect Jupiter in 1963, but none were clearly successful. Radar eventually was successful at detecting solid objects, like Jupiter's Galilean Moons and Saturn's rings, but not the planets themselves (as they are gas). Icarus, an Earth-crossing asteroid was detected in June of 1968 by several different observatories. Eventually satellites were launched and arrived at all of the planets in the solar system, and scientists are able to send and receive radio waves from them to judge the distances of planets.

▣ Math Behind Radar Ranging

The mathematics behind this concept is simple. It all involves distance = rate x time. All scientists have to do is know the speed of light (299,792,458 m / sec) and then the time it takes for the light waves to hit the planet and then bounce back. Then, they divide this time by 2 (because the light travels the distance from Earth to the planet twice). And from that they can tell how far away the object is.

Let d be the distance to the planet and t be the time that it takes for the radio waves to hit the planet and return. We know that $$ 2 \cdot d = 299,792,458 \frac{\text{m}}{\text{sec}} \cdot t $$ Now we need to make sure that our labels match so we will require t be given in seconds. Then we can say that $$ 2 \cdot d = 299,792,458 \frac{\text{m}}{\text{sec}} \cdot t \text{ sec}$$ We can then simplify and find that $$ 2 \cdot d = 299,792,458 \cdot t \text{ m} $$ and finally that $$ d = \frac{299,792,458 \cdot t}{2} \text{ m} $$ so we have the distance in meters to the star.

▣ Consequences of Radar Ranging

Radar echoes from Venus allowed the International Astronomical Union to adopt an exact value for the astronomical unit (AU). This value calibrates and is used to measure the distance with all other types of distance measurement in space. This is the basis of the cosmic ladder.

◰ Distance Modulus

▣ History of the Distance Modulus

Originally in ancient Greece, Hipparchus (160-127BC) started classifying stars into six classes based on their apparent brightness (or magnitude). The brightest stars he classified as first-class stars, the next faintest were second-class, and so on for six classes. These brightness classes are now known as apparent magnitudes and are generally denoted with m and a subscript, such as m_V with the subscript indicating that the apparent magnitude was obtained using a particular filter to get the measure of the brightness of a star (V is the closest filter to the human eye).You may not know this, but your eye is a logarithmic detector for light. This means that while your eyes would only perceive a change of 1 order of magnitude, this actually corresponds to a multiplicative factor of light intensity. This is good for our eyes but starts to involve logarithms in the calculations to stars. In the scale that Hipparchus used, a difference of 5 magnitudes indicated a scale factor of about 100 in light intensity. The logarithmic relationship between apparent magnitude and luminosity was published by Oxford astronomer, Norman R. Pogson, although it had been mentioned by others before him, and was accepted in 1887 in the Harvard College Observatory, but wasn't universally accepted until after 1905.

However, this relationship only tells us about how the bright the stars appear to be. It doesn’t tell us about how bright the stars are intrinsically. For that we use the absolute magnitude. Absolute magnitude is defined as the apparent magnitude of an object when viewed from 10 parsecs (3.26 light years) away. The absolute magnitude is denoted M with subscripts as used with the apparent magnitude. There are two ways to measure absolute magnitude, but one requires knowing the distance (which is what we are interested in). The second involves knowing the luminosity class (which is based on size of the star) and the spectral class (based on the temperature of the star).

Regardless, these tools allow us to compare two stars and their distances, but we still need a star to compare to. We compare them using the distance modulus which involves three different variables. M is the absolute magnitude of the star (when seen from 10 parsecs away), m is the apparent magnitude of the star (brightness that we observe) and r is the distance to the star in parsecs. The distance modulus is an equation that Jacobus Cornelius Kapteyn, a Dutch astronomer, introduced in 1902.

This was just another tool to compare measurements with the stellar parallax until later in the 20^th century, when Henrietta Swan Leavitt started classifying stars in the Large and Small Magellanic Clouds at the Harvard Observatory. Henrietta Swan Leavitt was the woman to identify a type of star that are known to have extremely regular pulses (periods of brightness and darkness) in 1908. These "standard candles" (lights that we know the brightness of and so can use to measure distance) are usually called Cepheid variable stars and are known for having a short period of between 1 to 50 days. In addition, she discovered that a Cepheid stars' period is directly related to its' luminosity or brightness. This allowed scientists to identify stars that we can easily find the distance to using the distance modulus, because the absolute magnitude can be found easily. One such star is Polaris or the North Star.

The distance modulus was further calibrated by Danish astronomer Ejnar Hertzsprung in 1913. He measured the parallax of several Cepheid stars which built the base for this start of measuring far distances using the distance modulus.

Here's a short video on the history and usage

▣ Math of the Distance Modulus

The way to describe the relationship between the brightness of two stars is denoted $$\frac{I_B}{I_A} = 2.512^{(m_A - m_B)}$$ or we can say that $$m_A - m_B = 2.5\cdot \log_{10}\left(\frac{I_B}{I_A}\right)$$ because of the rules of logarithms. The intensity of the light (I_A or I_B) is inversely proportional to the distance squared. This is called the inverse-square law. All this law says is that the brightness of a light source is inversely proportional to its' distance squared. Now, we can say that $$\frac{I_B}{I_A} = \left(\frac{d_A}{d_B}\right)^2$$ we can then take this and substitute it into the equation from above which will give us $$m_A - m_B = 2.5 \log_{10}\left(\frac{d_A}{d_B}\right)^2 $$ which can be simplified to $$m_A - m_B = 5 \log_{10}\left(\frac{d_A}{d_B}\right)$$ Then we assume a few things. First, we are going to look at one star instead of two. Thus, we will look at the difference in intensity between the star as we view it from Earth (m_A with d_A = d_A) and at a distance of 10 pc (M_A with d_A = 10 pc). We can substitute this second set of values in for m_B and d_B. Which leads us to be able to write that $$ m_A - M_A = 5 \cdot \log_{10}\left(\frac{d_A}{10}\right)$$ then if we require that d_A is specified in parsecs we can further simplify to say that $$m_A - M_A = -5 + 5 \log_{10}d_A$$ From there, we can use some algebra and exponential rules to rewrite the equation to solve for d_A and get that $$d_A=10^{0.2\cdot(m_A-M_A+5)}$$ which is the distance to star A in parsecs. This equation is simple and doesn’t correct for the interstellar reddening. Interstellar reddening is the idea that interstellar material (gas and dust) lies in-between us and the star and dims the star by absorbing and scattering light. But, that is the basic math behind the distance modulus formula.

▣ Using the Distance Modulus

It wasn't until 1918 that scientists realized that we could use this method on the scale of determining distances to galaxies. Harley Shapley of the Harvard Observatory College was the one to determine how the scale could be applied to determine the distance of clusters with cepheid stars in them.

Cepheid variable stars allows us to measure distances between 1 kiloparsec (1000 parsecs) and 50 megaparsec (50 million parsecs). This is the equivalent of 3.086 x 10¹⁶ kilometers to 1.543 x 10²¹ kilometers.

These stars aren't the only standard candle that scientists use today. We can also use the luminosity of a Type 1a supernovae because we know that at the peak of the outburst of a supernovae there is an absolute magnitude of -19.3 ± 0.03, but there are also many other ways that the distance modulus is used.

Type 1a Supernovae allow us to use this system to measure distances from 1 megaparsec (1 million parsec) to over 1000 megaparsec (1000 million parsec). This is the equivalent of a range of 3.086 x 10¹⁹ kilometers to 3.086 x 10²² kilometers.

Go ahead and see how big of a distance you can get.

◰ References

Butrica, A. J. (1996). To see the unseen: A history of planetary radar astronomy. Washington, DC: NASA. Retrieved from https://history.nasa.gov/SP-4218/sp4218.htm

Cepheid Variable Stars, Supernovae and Distance Measurement. (2018). Retrieved from https://lco.global/spacebook/cepheid-variable-stars-supernovae-and-distance-measurement/

Dutkevitch, D. (1998, October 7). Magnitudes and Distance. Retrieved from http://astro.wku.edu/labs/m100/mags.html

Elert, G. (2002). Mass of the Earth. Retrieved fromhttps://hypertextbook.com/facts/2002/SamanthaDong2.shtml

ESA Science & Technology: A history of Astrometry - Part II. (2013, December 12). Retrieved from http://sci.esa.int/gaia/53197-seeing-and-measuring-farther/

ESA Science & Technology: A history of Astrometry - Part III. (2017, March 22). Retrieved from http://sci.esa.int/gaia/53198-astrometry-in-space/

Henderson, T. (2012). Newton's Law of Universal Gravitation. Retrieved from https://www.physicsclassroom.com/class/circles/Lesson-3/Newton-s-Law-of-Universal-Gravitation

Hughes, D. W. (2006). The Introduction of Absolute Magnitude. Journal of Astronomical History and Heritage, 9(2), 173-179. Retrieved from http://adsbit.harvard.edu/full/2006JAHH....9..173H

Kraft, R. (1959). Pulsating Stars and Cosmic Distances. Scientific American, 201(1), 48-55. Retrieved from http://www.jstor.org/stable/24940328

Lienert, B. (1998). How do scientists measure or calculate the weight of a planet? Scientific American. Retrieved from https://www.scientificamerican.com/article/how-do-scientists-measure/

Luminosity Classes. (n.d.). Retrieved from http://csep10.phys.utk.edu/OJTA2dev/ojta/c2c/ordinary_stars/hr/classes_tl.html

Northon, K. (2014, April 10). NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space. Retrieved from https://www.nasa.gov/press/2014/april/nasas-hubble-extends-stellar-tape-measure-10-times-farther-into-space/

Pandian, J. D. (2016, January 30). How do you measure the distance between Earth and the Sun? Retrieved from http://curious.astro.cornell.edu/disclaimer/41-our-solar-system/the-earth/orbit/87-how-do-you-measure-the-distance-between-earth-and-the-sun-intermediate

Parallax and Distance Measurement. (2018). Retrieved from https://lco.global/spacebook/parallax-and-distance-measurement

Przyborski, P. (2009, July 7). Planetary Motion: The History of an Idea That Launched the Scientific Revolution. Retrieved from https://earthobservatory.nasa.gov/features/OrbitsHistory/page2.php

Saintonge, A. (2015, June 22). How do we weigh objects in space? (Beginner). Retrieved from http://curious.astro.cornell.edu/about-us/150-people-in-astronomy/space-exploration-and-astronauts/general-questions/933-how-do-we-weigh-objects-in-space-beginner

Smale, A. (2018, May 7). The Cosmic Distance Scale. Retrieved from https://imagine.gsfc.nasa.gov/features/cosmic/milkyway_info.html

Strobel, N. (2013, March 25). Planetary Science. Retrieved from https://www.astronomynotes.com/solarsys/s2.htm

Yirka, B. (2012, September 19). IAU votes to redefine the astronomical unit – giving it a constant value. Retrieved from https://phys.org/news/2012-09-iau-votes-redefine-astronomical-constant.html

◰ Images

Darling, D. (2016). Cosmic distance ladder [illustration]. Retrieved November 28, 2018, from http://www.daviddarling.info/encyclopedia/C/cosmic_distance_ladder.html

Kneller, G. (18th Century). Issac Newton [painting]. Retrieved December 6, 2018, from https://en.wikipedia.org/wiki/Isaac_Newton

NASA, ESA, A. Feild (STScI), and A. Riess (STScI/JHU). (2018, February 28). Three Steps to the Hubble Constant [illustration]. Retrieved from https://www.spacetelescope.org/images/opo1812a/

Noble, A. (2018). Generic Parallax Triangle [illustration].

Rosenberg, C., Weale, J. (early 19th Century). Henry Cavendish [painting]. Retrieved December 6, 2018, from https://www.npg.org.uk/collections/search/portrait/mw79897/Henry-Cavendish?LinkID=mp00810&role=sit&rNo=3

◰ Resources

Bayer, A., Bayer, M., Krištof, M., Pallová, K., & Okša, G. (2010). Solar System Scope [Interactive]. Retrieved November 28,2018, from https://www.solarsystemscope.com/

BBC (2014, February). How Big Is Space [Interactive]. Retrieved November 28, 2018, from http://www.bbc.com/future/bespoke/20140304-how-big-is-space-interactive/

Dolan, C. (2015, 16 January). Distance Modulus Calculator [Interactive]. Retrieved November 28, 2018, from http://csep10.phys.utk.edu/lightcone/demo/vlabs/labs/vlab20/distanceModCalculator.html

Henderson, T. (2012). Gravitational Fields Interactive [Interactive]. Retrieved November 28, 2018, from https://www.physicsclassroom.com/Physics-Interactives/Circular-and-Satellite-Motion/Gravitational-Fields/Gravitational-Fields-Interactive

Huang, C., Huang, H. (2012). The Scale of the Universe [Interactive]. Retrieved November 29, 2018, from http://scaleofuniverse.com/

Hudgins, D., Lee, K., & Prather, E. (2008, June 30). Radar Ranging [Interactive]. Retrieved November 28, 2018, from http://astro.unl.edu/naap/distance/radar.html

Khan, S. (2011). Cepheid variables 1[Video file]. Retrieved November 28, 2018, from https://www.khanacademy.org/science/cosmology-and-astronomy/stellar-life-topic/cepheid-variables/v/cepheid-variables-1

Las Cumbres Observatory. (2018, August 30). Stellar parallax and measuring distance [Video file]. Retrieved November 28, 2018, from https://www.youtube.com/watch?v=iwlMmJs1f5o

Noble, A. (2018, October 31) Investigate a Parallax [GeoGebra].

Noble, A. (2018, November 20) Mass in Space [Video file].

PBS Learning Media (2007, April 19). NOVA: What is a Planet? [Video file]. Retrieved November 28, 2018, from https://utah.pbslearningmedia.org/asset/hew06_vid_planetdefine/

UKAstronomy. (2016, February 27). Measuring the Universe [Video file]. Retrieved November 28, 2018, from https://www.youtube.com/watch?v=c9CBEAa2lII