It is important to understand modular arithmetic (also referred to as clock arithmetic) in order to understand affine substitution ciphers (as seen on this page: Affine Cipher ) as well as how cryptology is used today in what is known as RSA encryption (as seen on this page: Cryptology Today.)
When introducing modular arithmetic, it is beneficial to think of a clock. If someone asks you what time is it, you might respond by saying "3 o'clock." However, you could just as easily respond by saying "15 o'clock." 15 o'clock and 3 o'clock mean the same thing in our 24 hour world. If I told you it was 25 o'clock, you may look at me like I am crazy, but you could understand that I mean 1 o'clock. So, what we can say is that 25 o'clock = 1 + some multiple of 12 (which happens to be 24 in this case).
Alternatively, we can think of this as "the remainder when you divide 25 by 12 is 1." The way we write this mathematically is 25 ≡ 1 mod 12 (which is read "25 is congruent to 1 modulo 12"). The modulus can be thought of as the number of hours that we have broken the clock up into. We can create the following sets:
{...-12, 0, 12, 24, 36...}
{...-11, 1, 13, 25, 37...}
{...-10, 2, 14, 26, 38...}
...
{...-2, 10, 22, 34, 46...}
{...-1, 11, 23, 35, 47...}
From these sets, it is easy to see that 13 o'clock is the same as 1 o'clock, 23 o'clock is the same as 11 o'clock, and 46 o'clock is the same as 10 o'clock. We could also write 13 ≡ 1 mod 12, 23 ≡ 11 mod 12, and 46 ≡ 10 mod 12 All the numbers in each set are congruent to each other in mod 12. In general, we have the following:
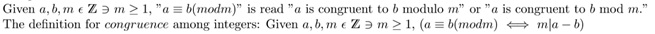
If we live in a 5 hour world, where m = 5, we can create the following sets:
{...-5,0, 5, 10,...}{...-4, 1, 6, 11...}
...
{...-1, 4, 9, 14...}
We can see that in a "5 hour world" or where the modulus is 5, 11 ≡ 1 mod 5 (because 5| 11 - 1) and 34 ≡ 4 mod 5 (because 5|34-4)
It may also be helpful to use the following applet: Clock Arithmetic Applet. It may also be helpful to do the following technology enhanced activity that I created to use while looking at the applet. (Activity Plans: Clock Activity Plans ) (Clock Arithmetic Task Sheet: Clock Task Sheet )