(Note, we will be using modular arithmetic here, so if you need a review, visit Modular Arithmetic )
Before we look at an affine cipher, it is important to quickly look at two other ciphers, namely additive ciphers and multiplicative ciphers.
In an additive cipher, also called a Caesar shift cipher, a plaintext character is replaced by another character whose position in the alphabet is a certain number of units away (mod 26) from that of the plaintext character. The number of units is called the key. Julius Caesar used an additive cipher with key = 3.
In a multiplicative cipher, Rather than adding a number (the key) to the position of a plaintext character, you multiply its position by a number (mod 26). So, if we were using a multiplicative cipher with key = 3, we could create the following table:

Note: J is the 10th letter in our alphabet. Our key is 3, so 3x10 = 30. 26|30 - 4. We can write this as 30 ≡ 4 mod 26. D is the 4th letter in our alphabet. Hence, J encrypts to D.
An affine cipher combines both additive and multiplicative ciphers by using two keys (say j and k). Letting p represent the position of the plaintext character in the alphabet, and c the position of the corresponding ciphertext character, we have the following equation:
c = j(p + k)(mod 26)In effect, an affine cipher is obtained by first applying an additive cipher with key k to the plaintext letter p. Once we obtain a new letter, we apply a multiplicative cipher with key j to the new text to produce the final ciphertext (Lewand).
Now, what if I need encrypt the message "meet me at" using and additive key of 11, and a multiplicative key of 7, or in other words, c = 7(p+11)(mod26). I could create the following table:
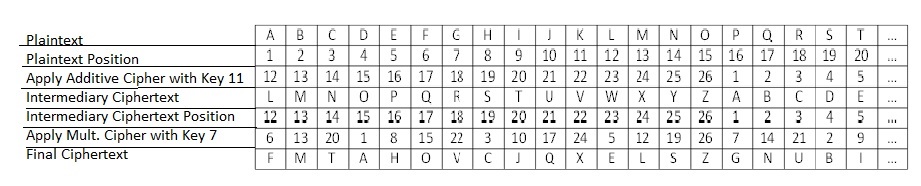
I first applied the additive cipher with key 11. This gave me an intermediary ciphertext. My message "meet me at" has become "XPPE XP LE." I then wrote the position for each letter of my intermediary ciphertext. I then applied a multiplicative cipher with key 7. My message "XPPE XP LE" has become my final ciphertext "LHHI LH FI." (Side note: How did I determine that L (position 12) corresponds to F (position 6)? First, I multiplied 12 by 7 (because that is the key I am using). 12x7=84. I then needed to determine what x equaled in the following: 84 ≡ x mod26. To do this I divided 84 by 26 and noted that 84⁄26 equals 3 with a remainder of 6. Because 6 is the remainder, I know that 84 ≡ 6 mod 26 because 26| 84-6. I then noted that the 6th letter in the alphabet is F.)