Instructions: Move the value "a" across the slider in both directions.
1. Look in the algebra window at the value called "b." What happens to "b" as you move the slider?
2. What do you think the relationship between "b" and "a" are?
3. What happens to "b" if "a" is less than 1?
4. Based on your previous knowledge of what a prime number is, add to your definition by stating what prime numbers
can be, and what they cannot be.
5. As "a" gets bigger, do you stop getting prime numbers? If we set the upper limit of "a" to a really big number like
5 million, do you think we would get prime numbers? What if our upper limit is infinity?
6. Is there a noticeable pattern for the prime numbers and when they occur?
Tasksheet and Lesson Plan PDF
Now try this one!
For example: The number 30 can be broken down into {5,2,3}. This can be shown several different ways.
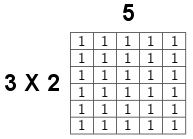What would a prime rectangle look like? Try it out!