Introduction

Not everyone likes mathematics. In fact, I would say that the vast majority of people have quite the dislike towards it. However, I have always liked math because of the order in it. Everything makes perfect sense. There aren’t any kind of's or maybe's in it because math just is. It has perfect order; it makes perfect sense. Well, at least most of the time. But what about when it’s not so clean and simple? What about the chaos and unpredictability? I started to wonder about that-about the chaos of math. So, here we are. Let’s talk about chaos theory, dynamic systems, and fractals. It may not all end nice and pretty, but I can promise you that it is interesting and worthwhile.

History and Background:

Chaos Theory had been explored a little bit in the past but it wasn't until 1961 that it really became its own thing. Edward Lorenz was a mathematician at MIT who created a weather model on his computer. This model "consisted of an extensive array of complex formulas that kicked numbers around” and required that one enter in different parameters to give a correct weather prediction (Abarim Publications). One day, Lorenz used an approximation of 3 decimal points instead of 6 places, thinking that this would only lead to minor, almost insignificant changes in the output. Turns out this was rather important, and when he ran it the second time with this approximation the entire system was changed. The image below taken from Chaos theory for beginners; an introduction, provides a visual of how this change might’ve looked:

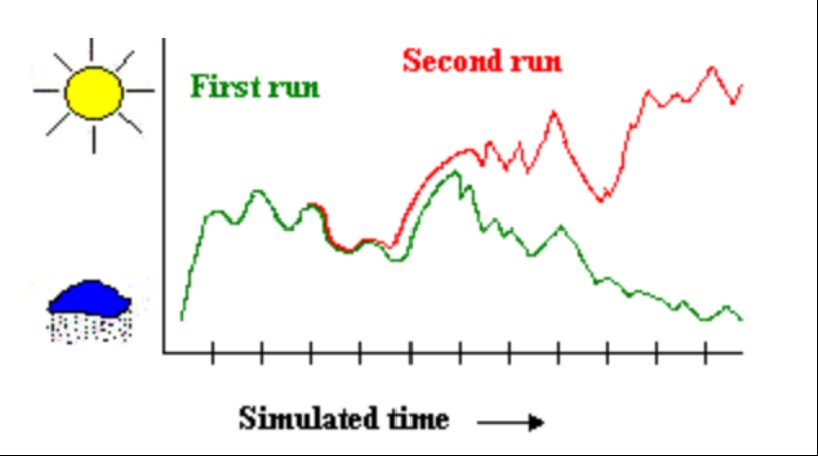
This was a significant discovery because at that time many mathematicians thought that “small variation at the start of a calculator would induce a small difference in the result, of the order of magnitude of the initial variation” (Oestreicher, 2007). Turns out they were very, very wrong.

Explanation of Mathematics

To start, let's understand exactly what chaos theory, dynamical systems, and fractals are and how they work together. Chaos theory, dynamical systems, and fractals are interconnected concepts that come together to reveal the underlying order within apparent disorder and the inherent structure in seemingly random patterns. The website Fractalfoundation.org explains that chaos theory focuses on the study of deterministic systems that exhibit sensitive dependence on initial conditions, meaning small changes in the starting conditions can lead to vastly different outcomes. This sensitivity to initial conditions is often observed in dynamic systems. “Simple nonlinear dynamical systems and even piecewise linear systems can exhibit a completely unpredictable behavior, which might seem to be random, despite the fact that they are fundamentally deterministic” (Wikipedia, 2023). Dynamic systems involve the study of how variables change over time, and chaos theory helps us understand the intricate and sometimes unpredictable behavior of these systems.

Fractals, as Haggit describes on HowStuffWorks (2021), are complex geometric shapes that exhibit self-similarity, meaning they contain smaller copies of themselves at different scales. These fractal patterns often emerge in chaotic and dynamic systems. As Clifford (2020) explains, the interplay between fractals and chaos theory can be seen in the fact that fractals are used to model chaotic systems and display their intricate structure. This connection between fractals and chaos theory allows scientists and mathematicians to represent and study complex, nonlinear phenomena that occur in dynamic systems.

Now for some of the mathematics behind all of this. In chaos theory, fractals provide a geometric representation of self-similarity across scales. The mathematics behind this self-similarity involves the use of recursive equations, iterated functions, and fractal dimension. Fractal dimension, as Haggit (2021) explains, is a concept that quantifies the "roughness" of a fractal, allowing mathematicians to characterize the intricate and complex structures that often arise in chaotic systems.

One of the fundamental mathematical tools in understanding fractals within chaos theory is the concept of the Mandelbrot Set, an iconic example of a fractal, as detailed in the article on nnart.org. The Mandelbrot Set is generated using a simple iterative formula that involves complex numbers, and it reveals a mesmerizing, infinitely detailed pattern. This mathematical exploration of the Mandelbrot Set exemplifies the intricate relationship between chaos theory and fractals, as it demonstrates how nonlinear dynamical systems can give rise to infinitely complex and self-replicating patterns. Below is given the graph and recursive formula of this set:

In essence, the mathematics behind chaos theory and fractals together offer a profound lens through which to explore the hidden beauty and structure in the apparent randomness and disorder of the natural world.

Fractal Tree Applet

If you would like to experiment with this basic fractal tree to understand how they work feel free!

Other Applets

Fractal Tree

Pendulum model

Pendulum Applet

Significance and Applications:

The significance of fractals in the world cannot be overstated. Fractals, as described in the HowStuffWorks article by Harris (2020), are found in diverse fields, from art and nature to technology and finance. In nature, they help describe and understand complex systems like turbulent fluid flow, the growth of plants, and the irregular shapes of coastlines. The significance also extends to art and design, where fractals have been used to create visually captivating images, architecture, and even music. In technology, fractals play a role in image compression, enabling efficient storage and transmission of visual data. Moreover, the financial world has found applications for fractals in understanding and modeling complex market behaviors, as discussed by Clifford on the Fractalerts website (2020). This widespread significance underscores the role of fractals in providing insights into the underlying structure of seemingly chaotic systems.