SEMESTER PROJECT
EXPLANATION OF MATHEMATICS
There are over 300 proofs of the Pythagorean theorem. Mathematics teacher Elisha Scott
Loomis (1852-1940) spent his life writing 371 proofs in his book The Pythagorean
Proposition, published in 1927 (Ratner, 2009). Others who have created their own proofs
of the theorem include Albert Einstein, Euclid, Leonardo da Vinci, and James Garfield.
Multiple videos and applets have been made on the subject as well. Consider this applet
by the user Skoledu which demonstrates two different geometric proofs.
GeoGebra Applet by user Skoledu
Albert Einstein wrote a proof of the Pythagorean theorem based on similar triangles
and their properties. He was twelve years old at the time, and his life was changed
because of the theorem. Years later, he used it in a fourth-dimensional form in the
Special Theory of Relativity and in the General Theory of Relativity, where Einstein
applied the Pythagorean theorem to three coordinates and set them equal to the
displacement of a ray of light (Ratner, 2009).
Euclid's Elements includes two proofs of the theorem, the first being Proposition 47
of Book I and the second being Proposition 31 of Book VI. The former relies on area
relations, while the latter is based on proportion. Proposition 31 of Book VI states,
''In right-angled triangles, the figure on the side opposite the right angle equals the
sum of the similar and similarly described figures on the sides containing the right
angle.'' Proposition 47 of Book I states, ''In right-angled triangles the square on the
side opposite the right angle equals the sum of the squares on the sides containing the
right angle.'' The latter is much simpler and is one of the most popular proofs of the
Pythagorean theorem. This proof has many names, including but not limited to, ''the
windmill,'' ''the bride's chair,'' ''franciscan's cowl,'' and ''the peacock's tail'' (Bogomolny, 2003).
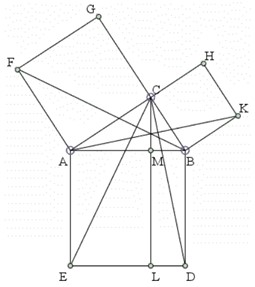
Figure 4: Sketch of Proposition 47 of Book I. The sum of the squares containing the
right angle is equal to the square opposite the right angle (Bogomolny, 2016).
Proposition 31 of Book VI from Euclid's Elements provides another proof of the
Pythagorean theorem. Because this proof is more complex than the proof Euclid's other
proposition, consider viewing Proof #7 from
Pythagorean Theorem and its Many Proofs by
Alexander Bogomolny. This website also contains a collection of 117 more proofs of the
Pythagorean theorem, if the reader is interested in learning more.
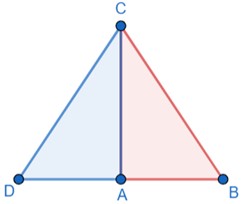
Figure 5: Euclid's proof of the converse of the Pythagorean theorem
Along with the two proofs of the Pythagorean theorem, Euclid provided a proof for the
converse of the theorem, which is used to test if a triangle is a right triangle.
Consider Figure 5 above. Given a triangle △ ABC, let a2 + b2 = c2, so (AB)2+(AC)2=(BC)2.
Then, draw the segment AD, which is equal to AB, perpendicular to AC. This forms the
right angle DAC. Connect point D to point C, creating the segment CD. Since AD=AB,
(AD)2=(AB)2. Then, adding (AC)2 to both sides, we get
(AD)2+(AC)2=(AB)2+(AC)2.
Now, because angle DAC is a right angle, we know that
(AD)2+(AC)2=(CD)2.
We also know that
(AB)2+(AC)2=(BC)2,
since that was given. Putting these two facts together gives
(CD)2=(BC)2,
so CD=BC. Now, because AD=AB and the segment AC is shared between
the two triangles, AD=AB, AC=AC, and CD=BC, so angle DAC is equal to angle BAC. Since
angle DAC is a right angle, this also means that angle BAC is a right angle. Therefore,
the triangle is a right triangle (Joyce, 1996).
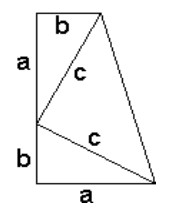
Figure 6: Pythagorean theorem proof by James Garfield
United States President James Garfield was interested in the Pythagorean theorem and
made a proof of his own utilizing the area of a trapezoid. As shown in Figure 6 above, the
area is given by the sum of the three triangles, so Area=\(\frac{1}{2}\) ab+\(\frac{1}{2}\)
ab+\(\frac{1}{2}\) c2=ab+\(\frac{1}{2}\) c2. Additionally,
the area of the entire trapezoid is shown by Area=\(\frac{1}{2}\)(height)(sum of bases)
=\(\frac{1}{2}\)(a+b)(a+b)=\(\frac{1}{2}\)(a2+2ab+b2). Then,
because the areas are equal, we get ab+\(\frac{1}{2}\) c2=\(\frac{1}{2}\)
(a2+2ab+b2). Simplifying this equation further gives
a2+b2=c2, the Pythagorean theorem (Gaskins, 2008).
At ten years old, Andrew Wiles used textbook methods to try to prove Fermat's Last
Theorem. This theorem states that there are no natural numbers x,y, and z such that
xn+yn=zn in which n is a natural number greater than
2 (Britannica). This theorem can be seen as the generalization of the Pythagorean
theorem. Later, Wiles studied the work of mathematicians who tried to prove it, but
he decided to leave Fermat's Last Theorem to study elliptic curves in his graduate
studies. His new study in elliptic curves provided a path to prove Fermat's Last
Theorem. Ratner (2009) wrote, ''Andrew Wiles' most famous mathematical result is that
all rational semi-stable elliptic curves are modular, which, in particular, implies
Fermat's Last Theorem.'' His proof took about seven years to complete, and in turn made
him famous.
Mathematicians across the globe have been fascinated by Pythagoras and the theorem named after him.
For hundreds of years, humans have been developing proof after proof to show that a2+b2=c2.
One common proof uses areas of the squares of the right triangle's legs to show that the sum of those
squares is equal to square of the hypotenuse. This proof has been duplicated several times
in different ways. Consider this original Geogebra applet which shows another way the areas of
the squares of the legs can be used to express the area of the hypotenuse.
Original GeoGebra Applet by Tyra Ah Kuoi
(In order for the applet to work, a must be less than b. However, if a>b in context,
the triangle can be reflected so that the longer side is along the bottom.)



