
First, let's look at what happens if we just guess at random. For simplicity's sake, we're going to look at a smaller version of the problem with only 10 prisoners who can each open 5 boxes.
The first prisoner (lets say this is prisoner #1) walks into the room and sees the following 10 boxes. What's the chance that the first box they open contains slip #1?

There are 10 boxes, each equally likely to contain slip #1. Therefore the chance that the first box the prisoner opens has their number is \(\frac{1}{10}\). Let's say we randomly picked box 4 to open first.
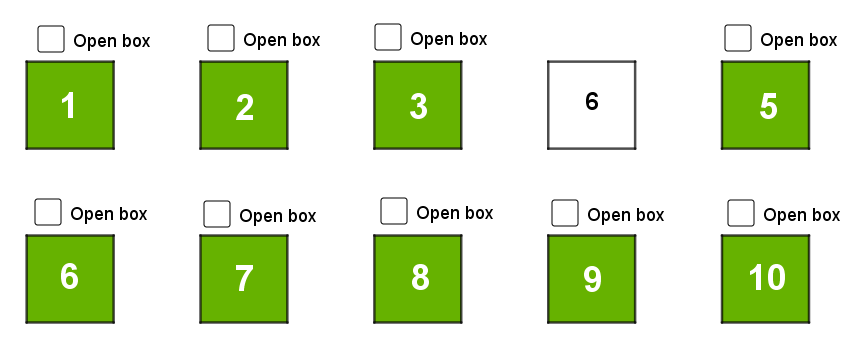
It shouldn't be a surprise that this box didn't have the number we wanted, the chance of that was only 10%. What's the chance the next box we open will have slip #1? There are 9 remaining boxes, each equally likely to contain #1, so the chance the next box we pick will be the right one is \( \frac{1}{9} \). Let's say we randomly selected box 2 to open next.
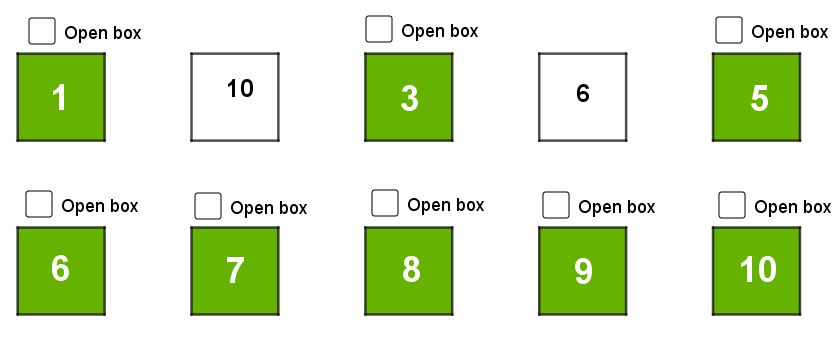
Still no luck. Again, we shouldn't be surprised, a chance of \( \frac{1}{9} \) means the odds are against us. Let's keep opening boxes at random until we run out of turns.
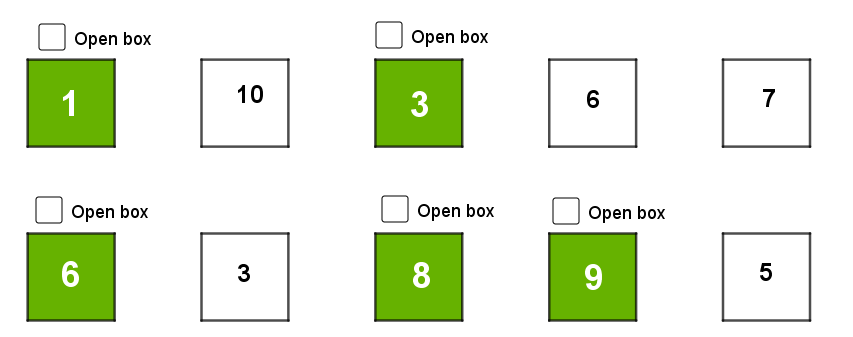
Uh oh, looks like we struck out. We got to open 5 out of the 10 boxes. It was equally likely that slip #1 would be in any of the 10 boxes, so we had a \( \frac{5}{10} = \frac{1}{2} \) chance of finding it. Alternatively, we could calculate our chance of failure. Since we had a \( \frac{1}{10} \) chance of success opening our first box, we had a \( \frac{9}{10} \) chance of failure. Then we had a \( \frac{8}{9} \) chance of failure for the second box and so on until we had a \( \frac{5}{6} \) chance of failure on the last box we were allowed to open.
The chance that we failed every time is \( \frac{9}{10} \times \frac{8}{9} \times \frac{7}{8} \times \frac{6}{7} \times \frac{5}{6} = \frac{15120}{30240} = \frac{1}{2}\). Once again, this means our chance of success is \( \frac{1}{2} \). All in all, that's not so bad! We can expect to find our number half the time. But wait, weren't there some other people on our team?
Each prisoner has the same chance of finding their individual number: \( \frac{1}{2} \). The problem is that we need every prisoner to find their own number. What are the chances of that? We can find the probability by multiplying each prisoner's chance of success together:
\( \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{2}^{10} = \frac{1}{1024} \)
Hmm, so our chances of success were slightly worse than one in a thousand, or about 0.098%. That's pretty bleak! What if we'd had the full 100 prisoners? Our chances of success would be \( \frac{1}{2}^{100} \approx 7.9 \times 10^{-31} \) which is too small even to comprehend. It doesn't look like guessing at random is a good strategy if we want to make it out of jail.
Remember, the challenge of this puzzle is to find a strategy that gives over a 30% success rate over many attempts. Clearly, guessing at random isn't going to do it. Let's go on and try to brainstorm some different strategies.
Back to top