"Symbols provide a blank background on which we may contemplate unadulterated meaning. They help us see [and] distinguish ingredients: the essentials from the disposable, the elements from the jumbles"
-- Joseph Mazur, 2014
What is a Symbol?
Let’s first discuss exactly what a symbol is. A basic definition may be that a symbol is a figure which holds deeper meaning. Mazur defines a symbol as being a "means of perceiving, recognizing, and creating meaning out of patterns and configurations drawn from material appearance or communication" (2014). He goes on to explain that the word symbol comes from the Greek word for "token" which comes from two other Greek words meaning "together" and "to throw" (Mazur, 2014). So, if we were to use the Greek definition of symbol, we would essentially be saying "to throw or to put together." Another definition to consider is "symbols are entities that stand for or take the place of something else" (Hiebert, 1988).
Application - Proof
Figure 1 depicts a proof of the theorem stating “The bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides” taken from Izen, (1998). We can observe some of the mathematical jargon within this proof and define it:
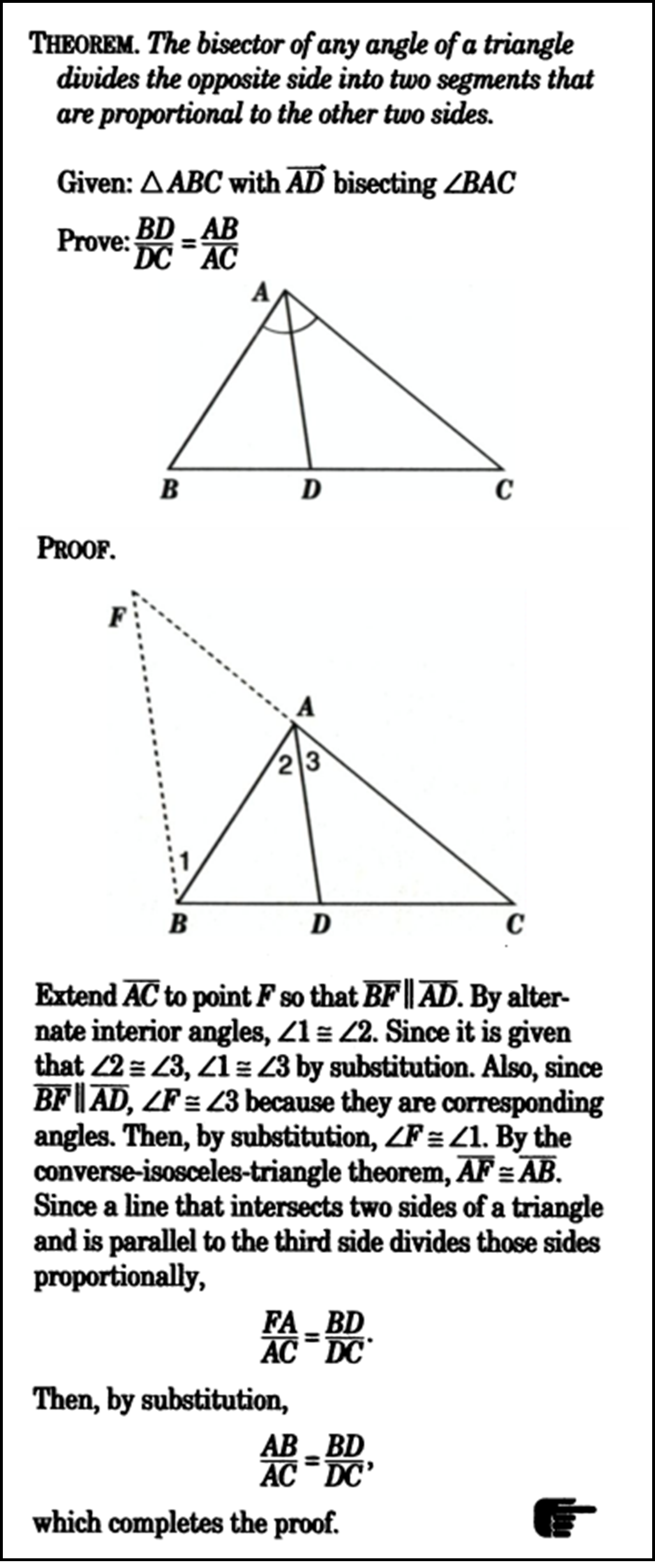
- Segment: A line with two end points.
- "$\triangle$": A reference to a triangle, followed by letters representing the vertices of that triangle. In this case $\triangle ABC$ a triangle that is constructed from points A, B, and C.
- "$\overrightarrow{AD}$": Line $AD$, or a line defined from point $A$ to point $D$.
- "$\angle BAC$": A reference to an angle that is constructed of the points $B$, $A$, and $C$ where point $A$ is the vertex of the angle on the triangle of interest.
- "$||$": is parallel to.
- "$\cong$": is congruent to.
- "$\overline{AB}$": A line segment formed from point $A$ to point $B$.
Figure 2 depicts a proof of the theorem stating "The bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides" taken from Izen, (1998). We can observe some of the mathematical jargon within this proof and define it:

- "$\exists$" means there exists.
- "!" in this case means unique. "!" may also mean factorial, but in this context it means unique.
- "ℝ" is the set of all real numbers.
- "$\in$" is read "is an element of."
- "$\ni$" is read "such that."
- "$\Rightarrow$" is read "implies.
- "$\nexists$" is read "there does not exist."
Application - Domain and Range
Defining the domain and range of a function is a prime example of using mathematical jargon. There are a couple of different ways to write the domain and range of a function. We can write it in interval notation or as set notation. Interval notation is a simple way of defining an interval on which a function’s domain or range rests. Interval notation using four main symbols: “[” includes a value, “)” does not include a value, “,” meaning “to”, and infinity “$\infty$”. An example would be: Domain: $(-\infty,4]$. That interval means that my function only has $x$ values from the smallest negative value up to 4 and it touches 4. Not all values can be included in interval notation, like this: Range: (0,4]. This means that my $y$ values can be anything between zero and four, but I cannot use the value zero because it does not have an $x$ value associated with it. Note that infinity will always use a parenthesis. Infinity is not a number, it is just a place holder for a number that is very, very large. We do not know what that number is, so we cannot include it. If we were to graph what we came up with, it may look something like this:
Set notation is a little different. It uses sets to help us define the numbers contained within the domain or range. Set notation also has some new symbols: “\{\}” represents a set, “:” is read where or such that (could also use “$|$” for such that), “$\in$” is read “is an element of”, “$\land$” is read “and”, and “$\ni$” is also read “such that”. Note that the colon is only used within the curly braces and defining a set of numbers that $x$ could be. Outside of this context, stick with “$\ni$”. Another rather important component of this notation is the actual set part. There must be a set of numbers that $x$ can be a part of. For example: $A =\{x:x\in ℤ \}$. Here I put in another symbol “ℤ”. This is the symbol for the set of integers. If we were to read set A we would say, “A is equal to the set of all $x$ such that $x$ is an element of the integers.
Interval notation can be defined by using set notation in the following manner: $a,b\;\in\mathbb{R}\ \ni a\le b,\;\left[a,b\right]=\{x:x\in ℝ \ \land a\le x\le b\}$ (Cangelosi, 2020). An English interpretation would be the elements $a$ and $b$ are elements of the set of Real Numbers such that a is less than or equal to $b$ and the closed interval from $a$ to $b$ is equal to the set of $x$ such that (or where) $x$ is an element of the set of real numbers and $a$ is less than or equal to $x$ and $x$ is less than or equal to $b$.
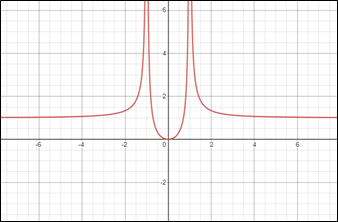
Using Figure 3, let’s state the domain and range in interval and set notation. This plot of $f\left(x\right)=\frac{x^2+2}{x^3-1}$ can help us see where the values are for the domain and range that our function does not have values for. Note that we have a horizontal asymptote at $y=0$ and a vertical asymptote at $x=1$. Our function does not stop as we travel along our x-axis to the left, nor does it stop on the right. Using our asymptotes and end behavior, we can construct the domain to be: \[\left(-\infty,1\right)\cup\left(1,\infty\right)\]. Note that parentheses were used instead of brackets because our function is undefined (not valid, there is not a value there) at the value of 1. Now for set notation: $\{x:x\ \in\; ℝ \ \land x\neq1\}$. Note that instead of values for a and b, we have used infinity, which has been encompassed in $ℝ$. Now that we have accounted for infinity, we just need to account for everything $x$ is not. Using similar logic, we can write out our range: \[\left(-\infty,0\right)\cup\left(0,\infty\right) and \{y:y\ \in ;ℝ \land y\neq0\}\]

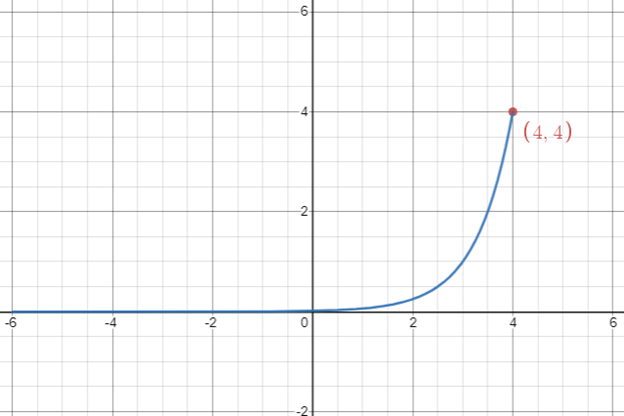
Now it is your turn. Using Figure 4, state the domain and the range of the function in both interval and set notation. The following questions might help guide you to finding the domain and range: Where is my function undefined both along the x-axis and the y-axis? What is the end behavior of the function?