Main page Assignment Semester Project Class Website
× Introduction Types of Optical Illusions Explanation of Mathematics Significance and Application Definitions Citations

Explanation of Mathematics



Even when we become aware of the phenomenon occurring we cannot unsee the illusion because that is how the brain is wired (National Geographic 2021).

In Hoffman's book (2000) called Visual Intelligence: How We Create What We See, Hoffman talks about how the brain interprets 2-dimensional images into 3-dimensional objects. 35 rules are presented by Hoffman on how our brains use our understanding of math to create these optical illusions. To understand the mathematics of these optical illusions, I will refer to and use only a few of Hoffman's rules listed below:

Literal Illusions

We technically see the world in 2-dimensional space, but with shadows, size, and perception we make 3-dimensional spaces in our minds. Literal illusions happen when we see silhouettes of objects that are like other objects. This means we can follow rule 16 (Hoffman 2000). If we take the example of the tree branch, each branch has concave cusps between each twig and are broken into individual parts at each twig connection. Once our brain automatically breaks the branch into parts it interprets the silhouette as a similar silhouette, one we are more familiar with, like a hand. The same principle is applied when looking at the pile of clothes in a dark room, we see the silhouette broken into separate pieces and connects it into a human-like form.

Physiological illusions

Rule 34 states that motion follows planar and rigid translations (Hoffman 2000). This afterimage effect happens because the stimulus of the image continues after looking away from the image. For example, with the waterfall afterimage effect, the rocks climb upwards where the stimulus, the water, was falling downwards. There is a lot of theory behind why this happens, it has been conceptualized that it is based on a fatigue of neuron groupings (Eagleman, 2001). Whatever the reason this occurs, the illusion being viewed is still created with math. Given rule 34, the motion is viewed as rigid and planar. The afterimage effect stays on the same plane that the stimulus was given, and the translation of certain points of stimuli maintain the same distance. The afterimage doesn't get bigger or smaller than the actual image. Hermann's Grid can be explained through rule 2 and rule 22. Through rule 22 we abrupt change of color from the black grid and the white lines means they reside on different surfaces. By rule two the coinciding white lines are coinciding in 3D or on the same plane. This leads to an effect called lateral inhibition, which causes a bright surround to an area appear darker and, conversely, a dark surround to an area appear lighter (Schrauf 1995).

Cognitive illusions

Ambiguous illusions

First looking at The Young Lady and The Old Lady the young lady and the old lady optical illusion. When we consider the rule 15 (Hoffman 2000), we divide the image into the concave cusps along the curvature. This would be under the nose/chin and the eye/wart. When broken into these parts the viewer then starts to see how the image can look like two things, because each part can represent different body parts. Necker's Cube 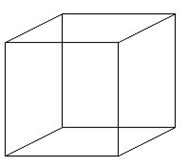illusion utilizes rules 1, 2 and 3 (Hoffman 2000). The lines that create the cube coincide in the 2-dimensional space and therefore are interpreted to coincide in 3-dimensonal. We know that the coinciding lines create a vertex to the cube oriented somewhere in space, then due to rule 3 the points of vertex are collinear, staying on the same continuous line, but it is up to our minds where on that line it is interpreted. Meaning it could be coming towards us or going away from us This is why the phenomenon of the cube jumping to different perspectives occurs.



Paradox illusions

The Penrose Stairs 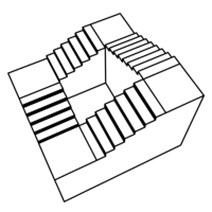is impossible in nature because a staircase goes always up or down. So how can you go in circles? Due to rule 2 and rule 14 (Hoffman 2000), we can see more clearly why this paradoxical staircase becomes an illusion. Based on rule 2 if lines coincide with one another they coincide in 3-dimensional space, therefore since the lines that create the stairs coincide, occur at the same time, with another all the stairs are connected to each other. The concave crease of the stairs, based on rule 14, shows each of the stairs bounded up and therefore each step is stepping up in nature. The Penrose Triangle follows rule 2 also since the lines coincide in the image, therefore they must connect in 3-dimensional space. The illusion can further be explained by rule 22, that the change in hue means that there is each surface is interpreted as a different surface. This means that all the surfaces are connected and different, which then by their orientation creates an object that is impossible.

Distorting illusions

The first example, the cafe wall can be explained with rule 2 and rule 3 (Hoffman 2000). We are using the opposite of the rule to understand this illusion. The black tiles' and white tiles' edges don't coincide with one another then they don't coincide in 3-dimensional space. Making the parallel gray lines to appear uneven or not parallel. Since the lines are interpreted as slanted, then by rule 3 they are also slanted in the 3-dimensional space.

The next example is Ponzo Illusion explained by rule 3 (Hoffman 2000). The edges of the horizontal lines on the railroad are collinear in the image, and they stay collinear in a 3-dimensional space. Therefore, the line that is longer than the collinear lines would stay long as it is moved up, and the shorter line would stay short as it is moved back. This means that the two lines cannot be the same size in 3-dimensional space, but are in fact the same length.

Fiction illusions

These illusions create an object when it isn't even there. Kanizsa triangle and Subjective Necker's Cube can both be explained by rule 11 (Hoffman 2000). These images are subjective to the viewer because they don’t actually appear within the image. Both the Kanizsa triangle and the Subjective Necker's Cube contain contains circles that have pointed concave cusps and therefore contain the triangle and cube between these circles.