Sets and Set Notation
What is a set? A basic understanding of set theory is essential to our understanding of the Continuum Hypothesis.
A set is simply any collection of objects - denoted with those objects contained in the set listed inside the brackets. The objects within a set are called elements.
For example, {socks}, {blue plates}, and {shapes} are all sets. As are {rocks, grasses, trees} and {January, February, March}.Doing math with socks or plates can be a bit tricky, so a traditional set is ordinarily a collection of numbers or functions: {1, 2, 3}, {-2, 6, 17, 48}.
To denote that an element is in a set we use the symbol \[\in\] So, to say x is an element of S, we write: \[x\in S\]
Often, we want to denote a set that contains infinite elements using an implied list.
For example, the set of natural numbers: {1, 2, 3, ...}, integers: {..., -2, -1, 0, 1, 2, ...}, rational numbers (those that can be expressed as a fraction with both the numerator and demomenator being integers), or real numbers.
These sets of numbers are used so often that they have their own special symbols:
However, we can run into trouble using implied lists. Given the set {2,4,...} I could mean two things: the set of even numbers, or the set of the powers of 2. To avoid confusion, we must be explicit.
Rather than using something like {even numbers}, we write: \[ \{ 2x | x \in \mathbb{Z} \}\] That is, all values 2x such that x is an integer. Alternatively, we might use \[ \{ x | x = 2^n , n \in \mathbb{N} \}\] That is, the set of the powers of 2.
In this way, we avoid any misinterpretation that could be caused by using an implied list.
Cardinality (Size of a Set)
The Cardinality of a set refers to how "big" the set is.
For a finite set, calculating the cardinality is as simple as counting the elements.
For example:
The cardinality of \[ \{ x | x \in \mathbb{N}, 1 \lt x \lt 3 \}\] is 1.
Two sets are the same size (have the same cardinality) if they can be put into a one-to-one correspondence with each other. That means each element in the first set can be uniquely mapped to an element in the second. This is called a bijection.
For example:
Here is a good visual: imagine that you are on a bus. Every seat is taken, and no one is standing. In this case, you know that there are the same number of people as seats - there is a bijection between the set of seats and the set of people. Therefore, the set of people and the set of seats are the same size.
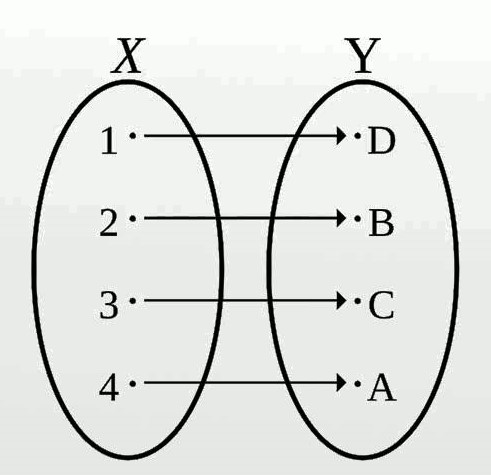
As another example, take S = {3, 7, 14, 26} and the T = {emu, snake, duck, gnu}.
The elements of S can be uniquely mapped to the elements of T:
Take another example: let S = {1, 2, 3} and T = {2, 4, 6}. For each element t \[\in\] T and s \[\in\] S, t = 2s. In this function, every s can be mapped to every t. Therefore, |S| = |T|.
Let's look at a nonexample. Let S = {1, - 1, 2, - 2, 3, - 3, 4, - 4} and T = {1, 4, 9, 16}. We could write a function: t = 2s, but while it is a function, it does not uniquely map the elements of one set to the other. For every element in T there are two possible elements in S: both a positive and a negative. Therefore, T and S do not have the same cardinality.
Finding the cardinality of infinite sets is where it gets interesting. Before we get to infinite sets, let's nail down what we mean by infinity.
What is infinity, really?
Infinity is very elusive. The human mind is not equipped to deal with infinity. We don't like infinity. And there is good reason for our natural dislike. When we start talking about infinity, we no longer have a physical world to rely on. We can't graph our functions, we can't draw our objects, we can't visualize our results in any way. If we rely on our intuition, we will be led astray. When dealing with finite numbers we could look around us and figure out at least the vague idea of what is going on. Now, like a submarine that has gone into the midnight zone in the deepest part of the ocean, we must rely on our mathematical instruments alone - regardless of what our intuition might say. The rules that worked for finite numbers don't apply in the infinite world.
When we talk about infinity, what often comes to mind is a number line that goes on and on until it reaches infinity.
Then it just... stops. But no! Numbers go on. There is always a bigger number.
It is helpful to think of infinity, not as a destination, but as a measure of how many numbers there are. It is a size - a concept - not a specific number that you can reach if you only go on long enough. Infinity is the size of a set of never-ending objects.
Next: Countable Infinity Back to Semester Project