Reflections
The mirroring of an object across a line of symmetry is the geometric transformation reflections. The line of symmetry marks the line of which the object is reflected over. This line could be placed anywhere about the cartesian plane, including inside the object itself.
Informally, reflections are sometimes called flips as an object or shape is "flipped" over a line of symmetry.
During this transformation the object should not alter in size or shape so it fulfills the definition of rigid transformations. The orientation may change due to the placement of the line of symmetry but the shape and size can not be manipulated throughout the transformation.
Examples of reflections that can be found in our daily life are the symmetry of a person’s face, butterfly wings, cars, and flipping images on an electronic device. Each of these examples have a line of symmetry that can be drawn within the object that reflects one side of the object perfectly to the other. When splitting the object in half with the line of symmetry, if one side is different from the other the transformation no longer meets the definition of the rigid transformation, reflection.
Essentially any object that is asymetric can be used as a nonexample of a reflection transformation. A specific example is a humans hand. We cannot define of line of symmetry on our hand is cannot be defined as reflective. Can you think of any nonexamples?
A neat concept with reflections is an object may not appear symmetric however with specific placement of the line of symmetry an object could statisfy the definition of reflections. An example of this could be a spoon. Placing the line perpendicular to the spoon handle the object is not symmetric but by placing the line of symmetry horizontally through the handle the spoon is now symmetric.
Here is an applet, titled "Looking in a Mirror", that can help you explore the properties of reflections. By checking the box "Line of reflection" (another name for the line of symmetry), a linear line will show of which you can reflect the original polygon across. The reflected polygon will show by the checking of the box "Polygon A' ". If you would like to try reflecting another polygon, select and drag the points of the original polygon to create a new shape!
Using these checkboxes explore how the coordinate points are effected by the transformation. Can you notice any patterns between the x and y coordinates of the original and reflected polygon?
Can you see any patterns of reflections when placing the line of reflection so it intersects the original polygon?
For further exploration of reflections, try this applet by created by Jon Ingram using Geogebra!
Informally, reflections are sometimes called flips as an object or shape is "flipped" over a line of symmetry.
During this transformation the object should not alter in size or shape so it fulfills the definition of rigid transformations. The orientation may change due to the placement of the line of symmetry but the shape and size can not be manipulated throughout the transformation.
Examples of reflections that can be found in our daily life are the symmetry of a person’s face, butterfly wings, cars, and flipping images on an electronic device. Each of these examples have a line of symmetry that can be drawn within the object that reflects one side of the object perfectly to the other. When splitting the object in half with the line of symmetry, if one side is different from the other the transformation no longer meets the definition of the rigid transformation, reflection.
A neat concept with reflections is an object may not appear symmetric however with specific placement of the line of symmetry an object could statisfy the definition of reflections. An example of this could be a spoon. Placing the line perpendicular to the spoon handle the object is not symmetric but by placing the line of symmetry horizontally through the handle the spoon is now symmetric.
Here is an applet, titled "Looking in a Mirror", that can help you explore the properties of reflections. By checking the box "Line of reflection" (another name for the line of symmetry), a linear line will show of which you can reflect the original polygon across. The reflected polygon will show by the checking of the box "Polygon A' ". If you would like to try reflecting another polygon, select and drag the points of the original polygon to create a new shape!
Using these checkboxes explore how the coordinate points are effected by the transformation. Can you notice any patterns between the x and y coordinates of the original and reflected polygon?
Can you see any patterns of reflections when placing the line of reflection so it intersects the original polygon?
For further exploration of reflections, try this applet by created by Jon Ingram using Geogebra!
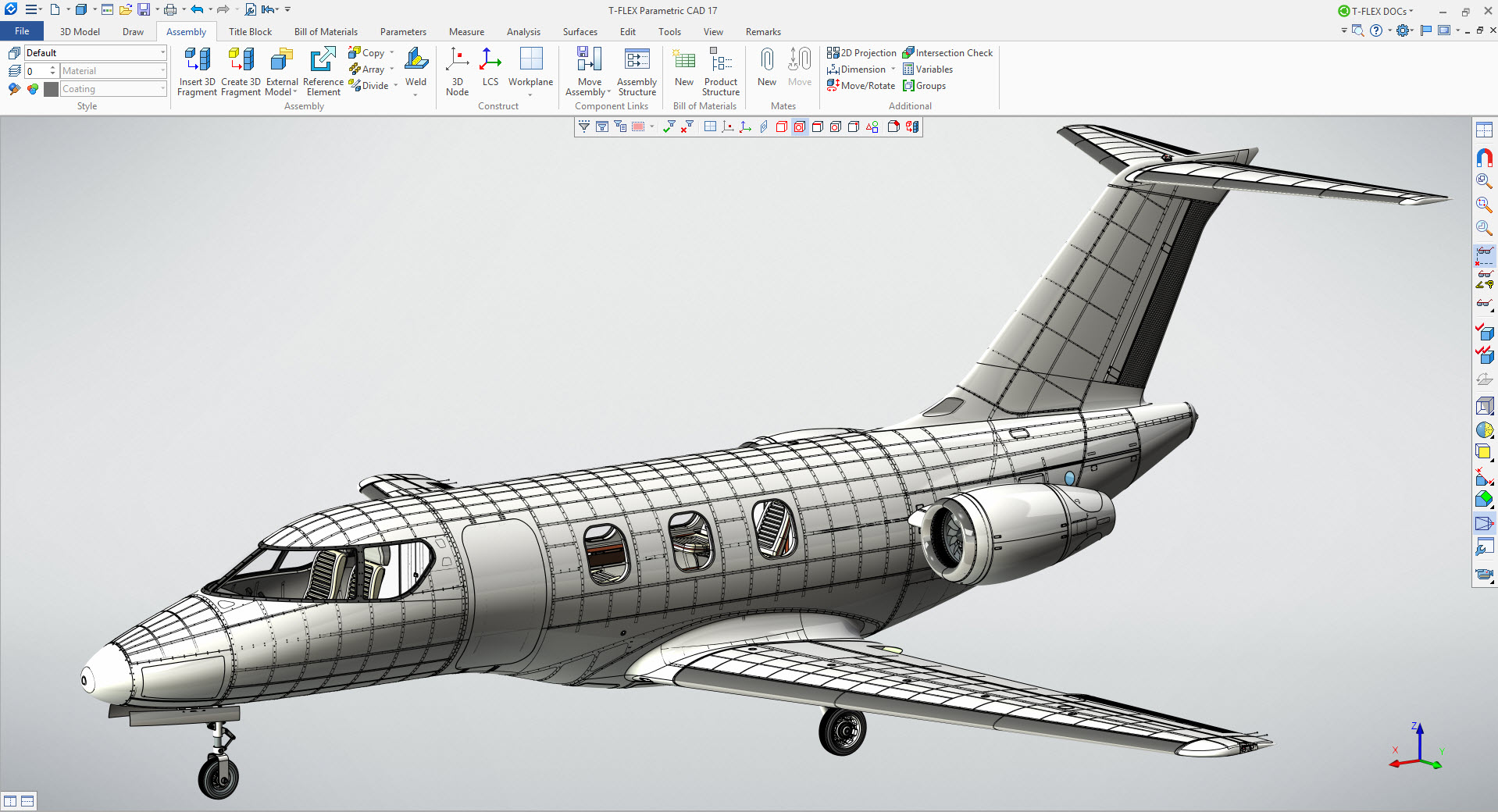
Another field of work that makes use of geometric transformations are engineers (CAD engineers). Engineers are responsible for the designing and manufacturing of new systems and devices in their individual department of engineering. Many of the objects engineers are responsible for designing are critical to the functioning of society like bridges, computers, phones, cars, airplanes, and much more. Throughout their designs engineers make use of geometric transformations. Engineers use the software CAD (Computer Aided Design) for designing various projects from complex machines to hot wheels.
The geometric transformation reflections are used to cut engineer's design time in half. Given a symmetric design, engineers can use reflections to reflect half of the design to complete the object saving the engineer's time and resources. The process of desining with CAD begins with engineers starting their design at an origin, they then draw out half of the objects outline and mark the distances of the outline to the origin. Once half of the design is completed and each of the outlines side's distances are known, the engineers simply select a line of reflection and the computer software completes the design through reflection. There are cases where reflections are done by hand however using CAD for designing is preferred. Reflecting the design through the software is quick and simple.
Check out this video to learn more about CAD - Computer Aided Design!
The geometric transformation reflections are used to cut engineer's design time in half. Given a symmetric design, engineers can use reflections to reflect half of the design to complete the object saving the engineer's time and resources. The process of desining with CAD begins with engineers starting their design at an origin, they then draw out half of the objects outline and mark the distances of the outline to the origin. Once half of the design is completed and each of the outlines side's distances are known, the engineers simply select a line of reflection and the computer software completes the design through reflection. There are cases where reflections are done by hand however using CAD for designing is preferred. Reflecting the design through the software is quick and simple.
Check out this video to learn more about CAD - Computer Aided Design!