Explore Surface Area and Volume
Surface Area and Volume are unique as they span such a wide range of topics and difficulty. This range can stem from the use of simple multiplication and formulas to more complex concepts of integration. As we explore the different levels of mathematics in Surface Area and Volume, connections can be drawn between a wide array of concepts. We will investigate some of the most common, regular three-dimensional shapes as well as how we could solve for the Surface Area and Volume of irregular three-dimensional shapes.
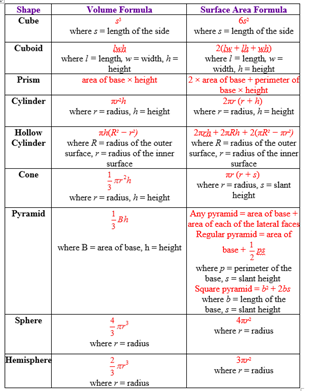
Some of the most common shapes used when teaching secondary students about Surface Area and Volume include that of a sphere, cylinder, and cone. Their formulas are expressed in the following table below for both Surface Area and Volume. If we pause for a second, we can take a more detailed look at an explanation for both the Surface Area and Volume in a few different shapes.

One example we can look at is the sphere and its unique three-dimensional shape. Archimedes realized that "the surface area of a sphere, was equal to the curved surface of a cylinder that has the same height and radius as said sphere" (Area). He was able to cut a sphere into two halves. That way he had a flat surface to work with. He then imagined placing one hemisphere with the flat side face down while fitting a cylinder around it. This meant that the circle at both ends of the cylinder were the same size as the bottom of the hemisphere. This also indicated that they shared the same height. Then he took transverse slices that formed rings as he cut down the cylinder. He took slices as small as he wanted and multiplied the areas of his rings by their depth to find the volume represented by the slices. He found that the volume of the rings added up to the volume of a cone that had the same radius and height as the cylinder. He conjectured that the volume of the hemisphere was equal to the volume of the cylinder minus the volume of the cone. In this way, he found that the volume of the cylinder was ((pi)r^2(h)) and the formula for the volume of a cone was known to be 1/3(pi)(r^2)h (Doc).
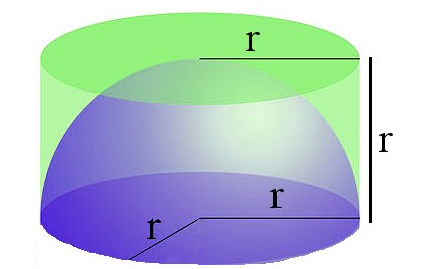
The formulas of Surface Area and Volume for the other common shapes can be explained in many different ways. Although we could spend countless time walking through the basics of deriving formulas for different shapes, lets take a closer look at a few of the more commonly looked at shapes. If we look at a cone, it takes the shape of a pyramid with a circle as its base which has a sloping side that come together at a center point. Therefore, to know its Surface Area and Volume, we need to know the radius of the base and the length of a side. The curved surface of the cylinder is represented by 2 * (pi) * r * h with height h and radius length 2r. The height is the same as the diameter, which is double the radius and thus we can rewrite the formula for the surface area of the sphere as 2 * (pi) * r * 2r and thus 4(pi)rē. If we are unsure of that information, we can use side length and the radius to find the cones height by application of the Pythagorean Theorem. Then we are ultimately able to find the total surface area as it is the sum of the area of the base and area of the side which is represented as (pi)r^2 + (pi)rs (Russell).
One other shape we can look at is a rectangular prism. When all sides are equal dimensions, then we have a cube. Finding the SA and V of either is possible as they use the same variables for their formulas. For each you need the length, width, and height. Thus, the Surface Area can be represented by the areas of the 6 sides as 2(lh) + 2(lw) + 2(wh) and the volume equals the lwh. We can see just by looking at these two three-dimensional shapes that there are close connections between the two formulas as they often require the same variables. However, if we run into situations with an arbitrary surface, then we need different ways to represent and find the Surface Area and Volume.
One of the major representations and relationships of Surface Area and Volume can be looked at through the use of integrals. This requires a lot of application to other concepts as well. Some of these concepts include the use of partial derivatives of parametric surfaces, double integrals, and using the cross product (Khan). In geometry, we often work with familiar and specific shapes that already have formulas given. However, as we move on and get into more real-world application, we see that often we are left to deal with an arbitrary surface that is defined by some parametric function. Through the use of a double integral, we are able to find the surface area of our object. The same can be said for volume. The process is a little different however as it involves the use of a triple integral (Kahn). The use of these functions enables us to expand the reach of Surface Area and Volume. This is where the work of Lebesgue was so important. This is also evidenced in the Disc and Washer method where integration is used to find the volume of different three-dimensional shapes.
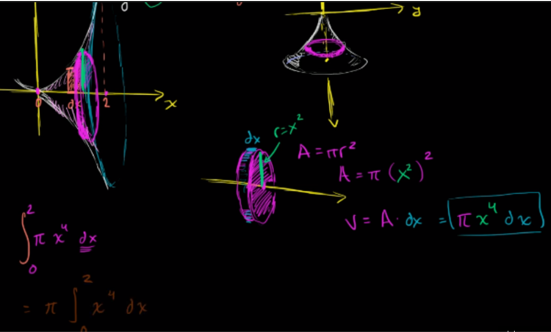
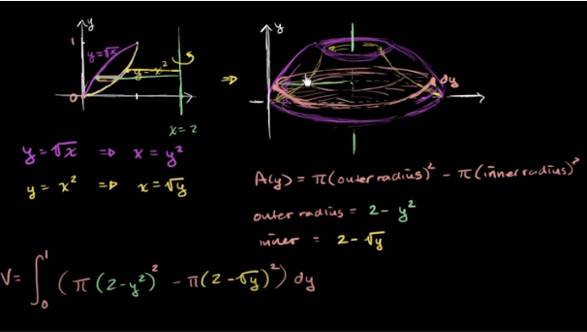
One can spend hours exploring within the realms of different arbitrary three-dimensional shapes. There are also other extensions of Surface Area and Volume. One that I find particularly interesting is known as the Pappus Centroid Theorem. This theorem states that "the surface area S of a surface of revolution generated by the revolution of a curve about an external axis is equal to the product of the arc lengths of the generating curve and the distance d1 traveled by the curve's geometric centroid x"(Wolfram). This is true where V=Ad_1=2(pi)sx.
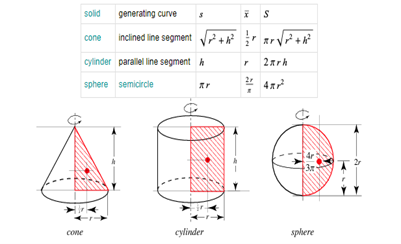
It is fascinating to also see how the second theorem of Pappus also applies as "the volume V of a solid revolution generated by the revolution of a lamina about an external axis is equal to the product of the area A of the lamina and the distance d2 traveled by the lamina's geometric centroid x" (Wolfram). V can be represented as V=Ad_2=2(pi)Ax.

Overall, we are able to observe that Surface Area and Volume extend from basic content and algebra to complex relations with integration and Reimann sums. The relationships and extensions of Surface Area and Volume allow for all types of scenarios and situations to be observed and solved. This was only a small sample size of the mathematics involved with Surface Area and Volume. These mathematics cover so much ground that the significance and applications they carry expand across numerous fields and events.