Leonardo Pisano was the first person to introduce others to the idea of the Fibonacci sequence. Leonardo Pisano is known by several different names including Leonardo Pisano Bigollo, Leonardo of Pisa, Leonardo Bonacci, and the most well-known one, Fibonacci. The name Fibonacci comes from the "truncated version of filius Bonacci meaning 'son of Bonacci'" (Watson, p. 5).
Fibonacci first introduced this sequence of numbers as a population problem with rabbits. He included this question in his book "Liber Abaci" when it was published in 1202, "A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?" (Supriatna, Carnia, & Ndii). The solution to this question is what we call the Fibonacci number or sequence, which was named such by Francois-Edouard- Anotole- Lucas around 1876 (Omotehinwa & Ramon, p. 631). The diagram depicting this pattern in the number of rabbits in each generation is below (Omotehinwa & Ramon, p. 630).
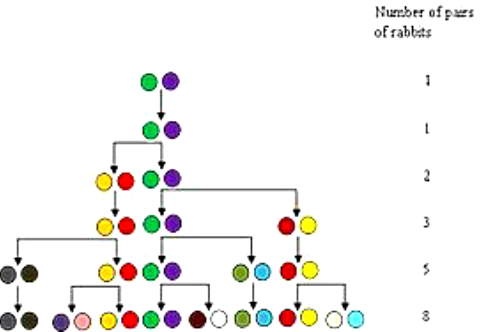
Fibonacci is also known because he "introduced the Hindu-Arabic system of numeration and arithmetic algorithm to Europe, which is the significant part out of the two contributions he is majorly remembered for" (Omotehinwa & Ramon, p. 630).
The Fibonacci sequence can be written in several different formats.
The sequence is written as 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... and it can also be written recursively as
Fn=Fn-1+Fn-2 where F0=F1=1 and n>1 (Fiorenza & Vincenzi).
Hundreds of years later in 1843, Binet discovered a closed formula that expresses the nth number in the Fibonacci sequence.
This formula can be expressed as:
(Bortner & Peterson)
or
(Supriatna, Carnia, & Ndii).
One of the most interesting features of the Fibonacci sequence is that when the larger of two consecutive terms is divided by the smaller of the two, the ratio gets closer and closer to 1.61803... which is the Golden Ratio, or Phi (Φ).
It was given the distinction of the Greek letter Phi (Φ) by an American mathematician, Mark Barr, who named it after the Greek sculptor Phidias, who used the principles of the golden section in all his sculptures (Omotehinwa & Ramon, p. 631).
This can be written as the limit of consecutive Fibonacci numbers:
(Fiorenza & Vincenzi).
The Golden Ratio goes by many different names including being called the "golden section by the ancient Greeks, golden proportion, mean ratio, divine proportion, golden mean or golden number" (Omotehinwa & Ramon, p. 631).
The Golden Ratio has many applications in mathematics and in several other fields of study including art, biology, and financial analysis (Supriatna, Carnia, & Ndii).