In grade school, we are taught about number lines. Now imagine a number line that contains a finite amount of numbers, let's say for example a number line containing 10 numbers starting at 0 and going to 9. Further, imagine that we take the line and turn it into a circle. This is what a "number line" in module arithmetic looks like, our specific example would be of modulus 10. Take a look below for visual reference!

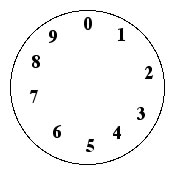
Modular arithmetic is a system of arithmetic for integers, where we are interested in what the remainder is when we divide two integers. We can think of this system as numbers that circle a modulus clock until they reach a certain value, called the modulus. In these cases, there is an operator called the modulus operator (we can abbreviate this as mod). Here is a general example: Suppose we have two integers a and n when we divide a and n we get (a/n)=q+r where q is an integer multiplier and r is an integer called the remainder. We can rewrite this in the form of a=n(q)+r . In modulus arithmetic this would look like (a mod n)=r . Note that if r=0 then a is a multiple of n . Here are some important definitions you'll need to know to understand modular arithmetic:
Definition 1: The group (Z n , +) is called the group of integers modulus n .
Definition 2. a mod n means the remainder when a is divided by n so a=qn+r where a, n, q, and r are elements of the set of all integers. (r-remainder)
Definition 3 Modulo Equivalence: a ≡ b mod n if and only if n |(a-b) (divisor is denoted as |). We will say that a and b are equivalent modulo n . We will also write modulo equivalence as a a ≡ b .
Definition 4: The set of all integers congruent to a modulus n is called the residue class [a] .
Definition 5: A relation of the form ax a ≡ b mod n is called a linear congruence.
Definition 6: Two numbers are relatively prime if their prime factorizations have no factors in common.
Definition 7 The Greatest Common Denominator: Z n
Definition 8: An inverse to a modulo m is an integer b such that ab ≡ 1(mod m)
Check out this applet to get familiar with modular clocks. This clock is in mod 3 and mod 9 clock see if you can deepen your understanding of modular arithmetic by interacting with the clock by finding the answer to these questions for the mod 3 clock (mod 9 clock has questions on the page):
30 mod 3=?
54 mod 3=?
100 mod 3=?
References for this page:
Khan, Sal. (n.d.) Journey into cryptography. Retrieved from https://www.khanacademy.org/computing/computer-science/cryptography
Dr. Finan, Marcel B. (n.d.). Arkansas Tech University MATH 4033: Elementary Modern Algebra: 11 Arithmetic Modulo n. Retrieved from https://faculty.atu.edu/mfinan/4033/absalg11.pdf
Cornell. (February 7, 2006). Everything You Need to Know About Modular Arithmetic. Retrieved from http://pi.math.cornell.edu/~morris/135/mod.pdf