Project: Quadratic Functions

Introduction

For the past two years, I have been a recitation leader for a college algebra course at Utah State University. Each semester I am surprised by the number of students who feel completely lost when we reach the section on quadratic functions. They struggle to understand that since a parabola is symmetric, the vertex of a parabola will always be located directly in the middle of the two zeros. I stumbled upon this disconnection during a test review day. My plan was to get my students attention by talking about toilet papering trees. I asked for volunteers who felt they had mastered the art of throwing toilet paper rolls over tree branches. Two students came to the front of the classroom and stood on opposite sides of the room. One student held one end of a roll of toilet paper and then tossed the roll to another student. I pointed out the beautiful parabola that the string of toilet paper made as it sailed across the room. We measured the distance between the two students and the maximum height that the toilet paper roll reached (we actually approximated this by measuring the height of the ceiling). When I declared that the maximum height was reached when the roll of toilet paper was halfway between the two students, one student asked, “Is that always the case?!” While this exercise led to a great discussion about the symmetry of parabolas, it made me realize how often students only focus on the minimum information they need to know in order to complete their math homework. I have come to realize that I was guilty of this as well until I gained a deep interest and love for mathematics. I chose this topic in hopes of finding new ways to teach my students about quadratic functions as well as to gain new insights into these extremely useful functions myself.

In the United States traditional public-school systems, it is common for children to first learn about graphing by looking at ordered pairs, then progressing to linear functions. For many of us, these topics are picked up fairly quickly, but when quadratic functions are introduced, mathematics seems to become much more difficult. We struggle to make the connection between the graphs that we draw on paper and application concepts such as maximizing the area of a rectangle, or how many seconds after the kickoff was the football at its maximum height.

Part of this confusion may arise if we see quadratic functions as a completely separate subject. We should be able to make a connection between linear functions and quadratic functions. We also need to be able to connect the graph of a parabola to the application concepts of maximization. Since the majority of word problems attempting to show applications of quadratic functions, and many of the real world application of quadratic funcitons are geometrically based, a geometric approach to quadratic functions may be more enlightening.

This website and article were written as a final project in a mathematics technology course I took at Utah State University during the fall of 2019. Many of the links in the menu above are part of other assignments for that course. While many of the assignments where used to construct this article, some were completed to show competence in specific technologies and other mathematical concepts. As you explore the remainder of this article, and my website, you will find many links to outside resources such as applets, podcasts, videos, and scholarly journals. The resources cited on this page can be found at the end of this article in the “References and Resources” section. However, a much larger list can be found under the “Assignments” tab on the menu above. My hope is that these resources will help to give insight and understanding in ways that I am unable to express in written form.

Historical Development and Background

Most public-school teachers use textbooks in which quadratic functions are taught as algebraic manipulations. However, the original development of quadratic functions came from ideas of geometrical algebra.

“Geometrical algebra is the branch of mathematics that is concerned with using geometrical concepts and proofs as the underpinnings of algebraic techniques.” While Greek mathematicians are usually credited with developing geometrical algebra, the basic ideas are clearly present in civilizations centuries earlier (Allaire, 308).

Rather than using quantities such as numbers or variables, geometrical algebra uses objects such as line segments to communicate. When two quantities are multiplied, the result is interpreted to be the area of a rectangle. Likewise, when three quantities are multiplied, the result is interpreted to be the volume of a right rectangular prism. This is the basis for our algebraic use of “square” and “cube” to represent second and third powers. The gap between geometrical algebra and computation algebra occurs when negative numbers arise. There is not an understandable way to visually show a line segment of negative length (Allaire, 308-9).

Many different civilization and individual mathematicians created their own ways of expressing and using quadratic equations. I will only give a brief overview of these methods here. For more information, consult this article.

Around 300 BCE, the father of geometry, Euclid, wrote his mathematical treatise The Elements. This collection of thirteen books includes the definition of a rectangle and the method for which the area of a rectangle is calculated. He explains how a rectangle becomes a square when the two adjacent sides are equal, and the area is therefore equal to the length squared (Byrne, 51). However, Euclid was not the first person to develop the idea of calculating areas. As early as 1750 BCE, the Mesopotamians were using their knowledge of areas of squares and rectangles to find positive solutions to quadratic equations (Heaton, 32). However, it appears that the Mesopotamians did not employ geometry into their work. Their scribes recorded algorithms and manipulation of numbers rather than drawings to depict their work (Allaire, 311).

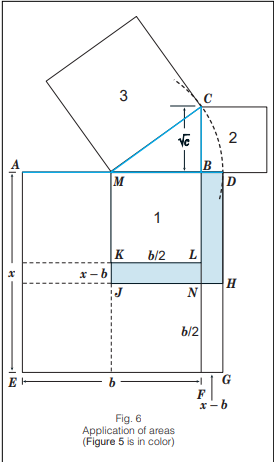
Between 500 and 600 BCE, the Greeks used a method for finding areas that they may have learned from Pythagoras. They arrange squares to create a right triangle, then employ the Pythagorean Theorem to conclude that the sum of the area of two rectangles is equivalent to the area of a square (Allaire 310-1).

During the ninth century, Muhammad ibn Musa al-Khwarizmi and other Islamic mathematicians geometrically demonstrated the process of “completing the square” to compute areas. At this point in time, negative numbers were still not being accepted by many mathematicians. It would be another three hundred years before negative coefficients or roots could be considered (Allaire, 312).

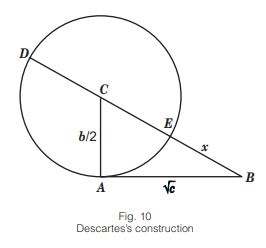
In the seventeenth century, René Descartes wrote his book La Géometrie where he describes the geometric method of constructing the solution of a quadratic equation. Like his predecessors, Descartes proof only shows the positive roots of the quadratic equation. He also employs the Pythagorean Theorem which creates some similarities between his proof and that of the Greeks (Allaire 312-3).

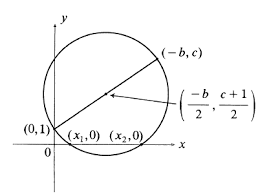
Finally, during the nineteenth century, Thomas Carlyle constructed a geometric proof showing all the real solutions of a quadratic equation as well as when solutions are imaginary (Allaire, 313).

Explanation of Mathematics

Let’s begin by using an algebraic approach to quadratic functions. Before we were introduced to quadratic equations, we explored linear functions. This should mean that we know the equation for a linear equation is \(y=mx+b\). We should be aware that the sum of two linear functions produces another linear function:

Since a, c, b, and d are constants, we can conclude that the sum of two constants produces another constant, so \((a+d)=m\) and \((c+e)=b\). Therefore \( f(x)=mx+b \). Likewise, the difference of two linear functions produces another linear function (Movshovitz-Hadar, 291). But what happens when two linear functions are multiplied? Is the product still a function? If so, is it linear? Let’s look at the following function:

Once again d,e,f, and g are constants, so adding or multiplying them by one another will produce another constant. If a and f are either both positive, or both negative constants, the resulting constant will be positive, if either a or f are negative, the resulting constant will be negative. We can therefore conclude:

Notice that since this passes the vertical line test, it is a function, but it is not a linear function because it curves. Rather, if we were to graph this function, we would see a parabola. If you are not yet familiar with parabolas, one of the key elements of parabolas are that they are symmetric. This means that when the vertex of the parabola is always located directly between the two roots (real or complex) and the y values are equivalent as we move equal units in the x directions away from the vertex. This Desmos Activity may help illustrate this point.

But what happens when the roots of the parabola are not real? At this point in our learning, we are usually given the “magical” vertex formula and told that it will always help us find the x-coordinate of the vertex of any parabola. We can then plug the x-coordinate into the quadratic function to find the y-coordinate of the parabola. But how does it work? How do we know that it will always find the x-coordinate of the vertex of ANY parabola?

One of the most effective methods for finding the roots of a parabola (real or complex) is to use the quadratic formula:

This formula is another one of those seemingly “magical” formulas that can actually be explained geometrically. If you want to see how, check out the video below.



Since the vertex is always located between the roots of parabola (both real and complex) we can find the midpoint of the two roots and that will give us the x-coordinate of the vertex! The quadratic formula gives the two roots of a parabola as \(-b + \sqrt{b^2-4ac} \over 2a\) and \(-b - \sqrt{b^2-4ac} \over 2a\). The midpoint can be found by finding the “average” of the two roots:

Notice that the denominators of the two roots are the same, so we can easily add the numerator which causes the square roots to cancel each other out. This leaves us with the following relationship:

Voila! The “magical” vertex formula is not quite as mysterious as you may have thought (Nebesniak, 430-2). Of course, those familiar with calculus may have already realized that it is easily derived by setting the derivative of the quadratic equation equal to zero and solving for x, but there are algebraic as well as geometric reasoning behind this formula as well.

At this point in college algebra classes, learning often shifts to real world applications. Scenarios such as throwing a ball may not be too difficult to visualize the correlation between the shape the ball makes in the air and a parabola, but how does the area of a rectangle relate to the graph of a parabola?

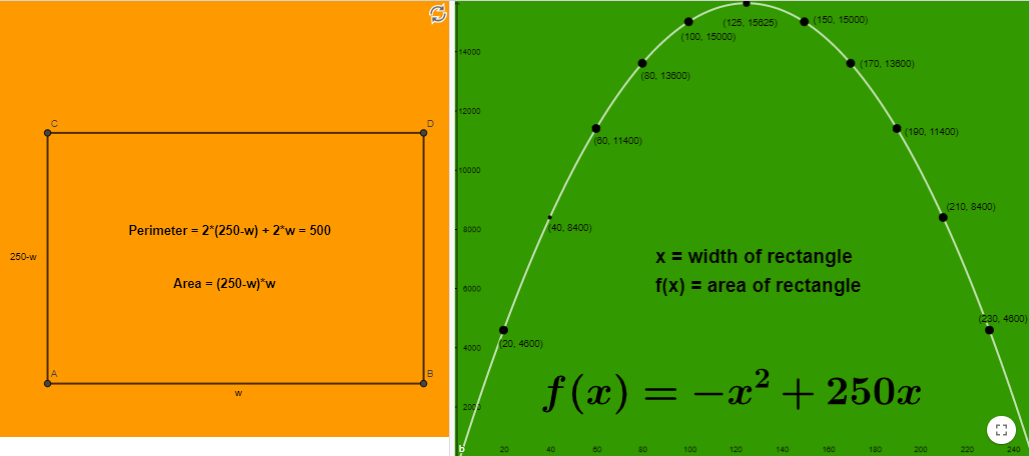
If we think about computing the area of a rectangle, we know the area is equal to the length multiplied by the width. What does this have to do with a parabola, you ask? If we want to create a rectangle with a set perimeter and a maximum area, the graph of a parabola may be more useful that you would initially expect. If the exact measurement of the sides of the rectangle are unknown as in the left side of the figure below, the area of the rectangle will be the length multiplied by the width. This gives us the quadratic equation found on the right side of the figure below. The graph of the quadratic function shows us the area (y) that results from each possible value for x. We can use the vertex formula to determine which value of x will give us the largest area. The graph on the right side of the figure below shows the correlation between the value selected for x (which is the width of the rectangle), and the area of the rectangle. Notice that if the perimeter is held constant, as the width of the rectangle increases so does the area up to the maximum, then the area decreases (Nielsen, 10).

Significance and Applications

One of the most commonly asked question in any math class is “When are we ever going to use this?” A couple of applications were mentioned in the above sections. Quadratic equations are used in a wide variety of applications. Any object that is thrown or kicked will make a parabolic shape in which we can measure the distance traveled, maximum height reached, time in the air, etc. To illustrate this point, watch the following two YouTube videos from the movie “October Sky”:

In these videos, Homer used quadratic equations (and a little Trigonometry) to determine the distance traveled by his rocket so he could locate it, then he used the same math to prove that there was no way his rocket could have started a forest fire. In another YouTube video, Jennifer Anderson shows many natural and manmade parabolas.



In order to construct the manmade parabolas, engineers had to be familiar with quadratic equations. This would have insured the structures would be able to withstand the weather and traffic issues in the designs.

What if rockets and engineering are not in your future? Does that mean quadratic functions are completely useless to you? Absolutely not! Quadratic functions are also used to assess business costs and the vertex formula is used to calculate the amount of product that a business should produce over a given time frame to maximize their profits. Also, as mentioned above, quadratic equations are used to calculate area and the vertex formula is used to figure out how to maximize the amount of area covered by a set perimeter.

Quadratic functions can be found all around us! So, the next time you are asked to use the quadratic formula, maximize the area of a rectangle, or simply driving in your car. Remember that you are doing more than just “solving for x” or looking at the cables on a suspension bridge. You are experiencing mathematics and making sense of things that used to puzzle ancient civilizations. While that may not always seem exciting, quadratic equations is just one step closer to mind blowing discoveries.

References & Resources

Allaire, P. R., & Bradley, R. E. (2001). Geometric Approaches to Quadratic Equations from Other Times and Places. Mathematics Teacher, 308-319.

Anderson, Jennifer. (2015, March 9). Retrieved October 7, 2019, from https://www.youtube.com/watch?v=He42k1xRpbQ&list=PLg7Z1a8SgF-7fOJLymR6BPn23ZBZOARa2&index=1.

Byrne, O. (1847). The First Six Books of The Elements of Euclid. London: William Pickering.

Heaton, L. (2017). A Brief History of Mathematical Thought. New York: Oxford University Press.

Lobato, J., Hohensee, C., Rhodehamel, B., & Diamond, J. (2012). Using Student Reasoning to Inform the Development of Conceptural Learning Goals: The Case of Quadratic Functions. Mathematical Thinking and Learning, 85-119.

MindYourDecisions. (2015, October 2). Retrieved December 4, 2019, from https://www.youtube.com/watch?v=EBbtoFMJvFc.

Movieclips. (2011, May 30). Retrieved October 7, 2019, from https://www.youtube.com/watch?v=udHB3tftPz4.

Movshovitz-Hadar, N. (1993). A Constructive Transition From Linear to Quadratic. School Science and Mathematics, 288-298.

Nebesniak, A., Burgoa, A. (2015). Developing the Vertex Formula Meaningfully. Mathematics Teacher, 429-433.

Nielsen, L. E. J., (2015). Understanding Quadratic Functions and Solving Quadratic Equations: An Analysis of Student Thinking and Reasoning. University of Washington, 1-167.

Smart, Myndi. (2019, December 3). Creating Quadratic Equations. Retrieved from https://www.geogebra.org/m/rcmhpn2c.

Smart, Myndi. "Figure 1." 2019. PNG.

TheFightinAnalyst. (2012, August 8). Retrieved October 7, 2019, from https://www.youtube.com/watch?v=RJhUWcpLfoc.

Will It Hit the Hoop? (n.d.). Retrieved December 4, 2019, from https://teacher.desmos.com/activitybuilder/custom/56e0b6af0133822106a0bed1.